题目内容
8.计算:(1)$\frac{s-2t}{3s}$•$\frac{6{s}^{2}}{s+2t}$; (2)$\frac{x-y}{x+y}$÷(x-y)2;
(3)$\frac{2a}{a+1}$+$\frac{2}{a+1}$; (4)$\frac{u-2v}{u+2v}$-$\frac{2}{{u}^{2}-4{v}^{2}}$;
(5)(x-2y3)-3; (6)($\frac{-3x}{{y}^{3}z}$)2.
分析 (1)根据分式乘法法则计算,约分即可;
(2)根据分式除法法则计算,约分即可;
(3)根据同分母分式加减法的运算法则计算;
(4)先通分,然后根据同分母分式加减法的运算法则计算;
(5)根据积的乘方运算法则计算;
(6)根据分式乘方法则计算.
解答 解:(1)$\frac{s-2t}{3s}$•$\frac{6{s}^{2}}{s+2t}$=$\frac{2{s}^{2}-4st}{s+2t}$;
(2)$\frac{x-y}{x+y}$÷(x-y)2=$\frac{x-y}{x+y}$•$\frac{1}{({x-y)}^{2}}$=$\frac{1}{{x}^{2}-{y}^{2}}$;
(3)$\frac{2a}{a+1}$+$\frac{2}{a+1}$=$\frac{2a+2}{a+1}$=2;
(4)$\frac{u-2v}{u+2v}$-$\frac{2}{{u}^{2}-4{v}^{2}}$=$\frac{{u}^{2}-4uv+4{v}^{2}-2}{{u}^{2}-4{v}^{2}}$;
(5)(x-2y3)-3=x6y-9=$\frac{{x}^{6}}{{y}^{9}}$;
(6)($\frac{-3x}{{y}^{3}z}$)2=$\frac{9{x}^{2}}{{y}^{6}{z}^{2}}$.
点评 本题考查的是分式的混合运算,掌握混合运算顺序、正确运用通分法则,合并同类项法则和约分法则是解题的关键,注意积的乘方、幂的乘方法则的正确运用.

练习册系列答案
相关题目
16.矩形两对角线交角为60°,且一条对角线与最短边的和为10,则对角线的长是( )
| A. | $\frac{10}{3}$ | B. | $\frac{20}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{25}{3}$ |
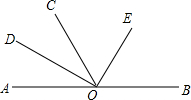 如图,O为直线AB上一点,∠A0D=∠COD,∠COE=∠EOB,若∠DOC:∠COE=2:3,求∠DOE,∠COD与∠COE的度数.
如图,O为直线AB上一点,∠A0D=∠COD,∠COE=∠EOB,若∠DOC:∠COE=2:3,求∠DOE,∠COD与∠COE的度数.