Question

14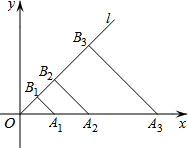．如图，在平面直角坐标系xOy中，点A₁，A₂，A₃，…，A_n在x轴的正半轴上，且OA₁=2，OA₂=2OA₁，OA₃=2OA₂，…，OA_n=2OA_n-1，点B₁，B₂，B₃，…，B_n在第一象限的角平分线l上，且A₁B₁，A₂B₂，…，A_nB_n都与射线l垂直，则B₁的坐标是（1，1），B₃的坐标是（4，4），B_n的坐标是（2^n-1，2^n-1）．

Answer 1

分析 根据规律得出OA₁=2，OA₂=4，OA₃=8，OA₄=16，OA₅=32，所以可得OA_n=2ⁿ，由题意知△OA_nB_n是等腰直角三角形，所以Bn的坐标为（$\frac{1}{2}$×2ⁿ，$\frac{1}{2}×{2}^{n}$）即（2^n-1，2^n-1），进而解答即可．

解答 解：如图，由题意知，△OA_nB_n是等腰直角三角形，
根据规律得出OA₁=2，OA₂=4，OA₃=8，OA₄=16，OA₅=32，所以可得OA_n=2ⁿ，
∴所以Bn的坐标为（$\frac{1}{2}$×2ⁿ，$\frac{1}{2}×{2}^{n}$）即（2^n-1，2^n-1），
∴B₁的坐标是（1，1），B₃的坐标是（4，4），B_n的坐标是（2^n-1，2^n-1）．
故答案为：（1，1）；（4，4）；（2^n-1，2^n-1）．

点评 此题考查一次函数图象上点的坐标，关键是根据规律得出OA_n=2ⁿ进行解答．