题目内容
五边形ABCDE∽五边形A′B′C′D′E′,∠A=120°,∠B′=130°,∠C=105°,∠D′=85°,则∠E= .
考点:相似多边形的性质
专题:
分析:首先根据相似多边形的性质得到∠B=∠B′=130°,∠D=∠D′=85°,然后根据五边形的内角和为540°求得未知的角即可.
解答:解:∵五边形ABCDE∽五边形A′B′C′D′E′,
∴∠B=∠B′=130°,∠D=∠D′=85°,
又∵五边形的内角和为540°,
∴∠E=540°-∠A-∠B-∠C-∠D=100°,
故答案为:100°.
∴∠B=∠B′=130°,∠D=∠D′=85°,
又∵五边形的内角和为540°,
∴∠E=540°-∠A-∠B-∠C-∠D=100°,
故答案为:100°.
点评:本题考查了相似多边形的性质,解题的关键是了解相似多边形的对应角相等,难度较小.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
美国NBA职业篮球赛的两支队伍在本赛季已进行了5场比赛,根据统计,两队5场比赛得分的频数分布直方图如下所示,则得分方差较小的队伍是( )


| A、甲 | B、乙 | C、一样大 | D、无法确定 |
若(x+m)(x+n)=x2-6x+5,则( )
| A、m,n同时为负 |
| B、m,n同时为正 |
| C、m,n异号 |
| D、m,n异号且绝对值小的为正 |
 如图,AC⊥DE,垂足为O,∠B=35°,∠E=25°,求∠A的度数.
如图,AC⊥DE,垂足为O,∠B=35°,∠E=25°,求∠A的度数.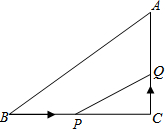 如图,在△ABC中,∠C=90°,BC=16cm,AC=12cm,点P从B出发沿BC以2cm/s的速度向C移动,点Q从C出发,以1cm/s的速度向A移动,若P、Q分别从B、C同时出发,设运动时间为ts,当为何值时,△CPQ与△CBA相似?
如图,在△ABC中,∠C=90°,BC=16cm,AC=12cm,点P从B出发沿BC以2cm/s的速度向C移动,点Q从C出发,以1cm/s的速度向A移动,若P、Q分别从B、C同时出发,设运动时间为ts,当为何值时,△CPQ与△CBA相似? 如图,在边长为1的小正方形组成的方格纸上,将△ABC(A、B、C为格点)绕着点C顺时针旋转90°.
如图,在边长为1的小正方形组成的方格纸上,将△ABC(A、B、C为格点)绕着点C顺时针旋转90°.