题目内容
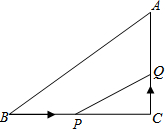如图，在△ABC中，∠C=90°，BC=16cm，AC=12cm，点P从B出发沿BC以2cm/s的速度向C移动，点Q从C出发，以1cm/s的速度向A移动，若P、Q分别从B、C同时出发，设运动时间为ts，当为何值时，△CPQ与△CBA相似？考点：相似三角形的判定
专题：动点型
分析：分CP和CB是对应边，CP和CA是对应边两种情况，利用相似三角形对应边成比例列式计算即可得解．
解答：解：CP和CB是对应边时，△CPQ∽△CBA，
所以，
=
，
即
=
，
解得t=4.8；
CP和CA是对应边时，△CPQ∽△CAB，
所以，
=
，
即
=
，
解得t=
．
综上所述，当t=4.8秒或
秒时，△CPQ与△CBA相似．
所以，
| CP |
| CB |
| CQ |
| CA |
即
| 16-2t |
| 16 |
| t |
| 12 |
解得t=4.8；
CP和CA是对应边时，△CPQ∽△CAB，
所以，
| CP |
| CA |
| CQ |
| CB |
即
| 16-2t |
| 12 |
| t |
| 16 |
解得t=
| 64 |
| 11 |
综上所述，当t=4.8秒或
| 64 |
| 11 |
点评：本题考查了相似三角形的判定，主要利用了相似三角形对应边成比例，难点在于分情况讨论．
练习册系列答案
相关题目
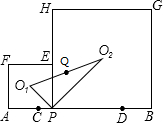如图：已知AB=10，点C、D在线段AB上且AC=DB=2；P是线段CD上的动点，分别以AP、PB为边在线段AB的同侧作正方形APEF和正方形PBGH，点O1和O2是这两个正方形的中心，连接O1O2，设O1O2的中点为Q；当点P从点C运动到点D时，则点Q移动路径的长是
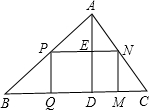如图，△ABC是一块锐角三角形材料，BC=120mm，高AD=80mm，要把它加工成一矩形零件，使矩形一边在BC上，其余两个顶点分别在AB、AC上．
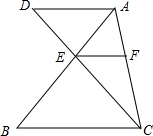如图所示，在△ABC和△CAD中，DA∥BC，CD交AB于E，且AE：EB=1：2，EF∥BC交AC于F，S△ADE=1，求S△AEF和S△BCE．
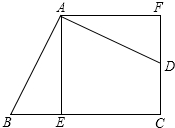如图，四边形ABCD的∠BAD=∠C=90°，AB=AD，AE⊥BC于E，△BEA旋转后能与△DFA重合．
如图，在△ABC中，AB=AC=30cm，DE是AB的垂直平分线，分别交AB、AC于D、E两点．