题目内容
AB是圆O的直径,C为圆上任意的一点,过C的切线分别与过AB两点的切线交于P、Q,已知AP=1,BQ=9,求圆O的半径.
考点:切线的性质
专题:
分析:本题根据题意画出图形,利用切线的性质定理得到PA=PC,QB=QC,再构造勾股定理即可得到答案.
解答: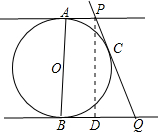 解:根据题意画图如下,过点P作PD⊥BQ,垂足为D,
解:根据题意画图如下,过点P作PD⊥BQ,垂足为D,
∵AP、BQ是⊙O的切线,且AB是⊙O的直径,
∴AP⊥AB,BQ⊥AB
∴AP∥BQ,
又∵PD⊥BQ,
∴四边形APBQ是矩形,
∴AB=PD,AP=BD=1,
∴DQ=8,
又∵PQ是⊙O的切线,
∴CP=AP=1,QC=QB=9,
∴PQ=10,
∴PD=
=
=6,
∴⊙O的半径是6.
 解:根据题意画图如下,过点P作PD⊥BQ,垂足为D,
解:根据题意画图如下,过点P作PD⊥BQ,垂足为D,∵AP、BQ是⊙O的切线,且AB是⊙O的直径,
∴AP⊥AB,BQ⊥AB
∴AP∥BQ,
又∵PD⊥BQ,
∴四边形APBQ是矩形,
∴AB=PD,AP=BD=1,
∴DQ=8,
又∵PQ是⊙O的切线,
∴CP=AP=1,QC=QB=9,
∴PQ=10,
∴PD=
| PQ2-DQ2 |
| 102-82 |
∴⊙O的半径是6.
点评:本题主要考查对切线长定理的理解和掌握,能根据切线长定理得出PA=PC、QC=QB是解此题的关键.

练习册系列答案
相关题目
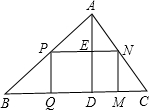 如图,△ABC是一块锐角三角形材料,BC=120mm,高AD=80mm,要把它加工成一矩形零件,使矩形一边在BC上,其余两个顶点分别在AB、AC上.
如图,△ABC是一块锐角三角形材料,BC=120mm,高AD=80mm,要把它加工成一矩形零件,使矩形一边在BC上,其余两个顶点分别在AB、AC上.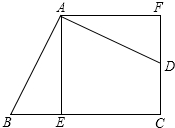 如图,四边形ABCD的∠BAD=∠C=90°,AB=AD,AE⊥BC于E,△BEA旋转后能与△DFA重合.
如图,四边形ABCD的∠BAD=∠C=90°,AB=AD,AE⊥BC于E,△BEA旋转后能与△DFA重合. 如图,在△ABC中,AB=AC=30cm,DE是AB的垂直平分线,分别交AB、AC于D、E两点.
如图,在△ABC中,AB=AC=30cm,DE是AB的垂直平分线,分别交AB、AC于D、E两点.