题目内容
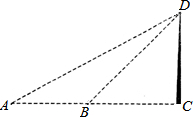 如图所示,在上海黄浦江西岸一点B处,测得东方明珠电视塔尖D的仰角为45°,后退20m到A处,测得塔尖D的仰角为30°,A、B、C在同一直线上,求电视塔的高度.
如图所示,在上海黄浦江西岸一点B处,测得东方明珠电视塔尖D的仰角为45°,后退20m到A处,测得塔尖D的仰角为30°,A、B、C在同一直线上,求电视塔的高度.考点:解直角三角形的应用-仰角俯角问题
专题:
分析:根据∠DBC=45°,得出BC=CD,设DC=x,根据∠BAD=30°,AB=20m,得出AC=20+x,再根据正切定理即可得出答案.
解答:解:∵∠DBC=45°,
∴∠BDC=45°,
∴BC=CD,
∵∠BAD=30°,
设DC=x,
∵AB=20m,
∴AC=20+x,
∴tan30°=
=
,
∴x=(10
+10)m;
∴电视塔的高度是(10
+10)m.
∴∠BDC=45°,
∴BC=CD,
∵∠BAD=30°,
设DC=x,
∵AB=20m,
∴AC=20+x,
∴tan30°=
| DC |
| AC |
| x |
| x+20 |
∴x=(10
| 3 |
∴电视塔的高度是(10
| 3 |
点评:本题考查了解直角三角形的应用,解答本题的关键是根据仰角构造直角三角形,利用三角函数的知识求解,难度一般.

练习册系列答案
相关题目
下列分解因式错误的是( )
| A、x2-2xy+y2=(x-y)2 |
| B、x3-x2+x=x(x2-x) |
| C、x2y-xy2=xy(x-y) |
| D、x2-y2=(x-y)(x+y) |
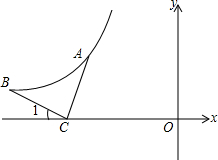 如图,反比例函数y=
如图,反比例函数y= 在一个直角三角形铁皮上剪下一块正方形,并使正方形面积尽可能大,正方形的面积是多少?(提示:连接DB)单位:厘米.
在一个直角三角形铁皮上剪下一块正方形,并使正方形面积尽可能大,正方形的面积是多少?(提示:连接DB)单位:厘米. 已知在平行四边形ABCD中,E、F分别是边AB、AD上的点,EF与对角线AC交于点P,若
已知在平行四边形ABCD中,E、F分别是边AB、AD上的点,EF与对角线AC交于点P,若 a、b在数轴上对应的点如图所示:
a、b在数轴上对应的点如图所示: