题目内容
已知:首项系数不相等的两个方程:(a-1)x2-(a2+2)x+(a2+2a)=0和(b-1)x2-(b2+2)x+(b2+2b)=0(其中a,b为正整数)有一个公共根,求a,b的值.
考点:一元二次方程的解
专题:
分析:分别求得两个方程的根,然后结合已知条件得到关于a、b的数量关系,再由限制性条件“a,b为正整数”来求a、b的值即可.
解答:解:由方程:(a-1)x2-(a2+2)x+(a2+2a)=0,得
[(a-1)x-(a-2)](x-a)=0,
解得 x1=
,x2=a.
同理可由方程(b-1)x2-(b2+2)x+(b2+2b)=0 得
x1=
,x2=b.
∵a-1≠b-1,即a≠b,且a、b为正整数,两个方程有一个公共根,
∴
=b,
则b=1+
,
∴a-1=1或3,
则a=2,b=4;或a=4,b=2.
[(a-1)x-(a-2)](x-a)=0,
解得 x1=
| a+2 |
| a-1 |
同理可由方程(b-1)x2-(b2+2)x+(b2+2b)=0 得
x1=
| b+2 |
| b-1 |
∵a-1≠b-1,即a≠b,且a、b为正整数,两个方程有一个公共根,
∴
| a+2 |
| a-1 |
则b=1+
| 3 |
| a-1 |
∴a-1=1或3,
则a=2,b=4;或a=4,b=2.
点评:本题考查了一元二次方程的解的定义.解题时,要注意a、b是互不相等的正整数.

练习册系列答案
相关题目
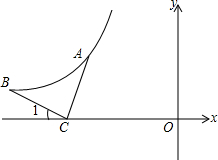 如图,反比例函数y=
如图,反比例函数y= 如图,点A、B、C、D为⊙O上的点,∠ABC=90°,若AD=8,tan∠DBC=
如图,点A、B、C、D为⊙O上的点,∠ABC=90°,若AD=8,tan∠DBC=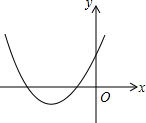 已知二次函数y=ax2+bx+c的图象如图所示,则
已知二次函数y=ax2+bx+c的图象如图所示,则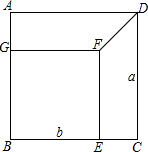 如图,将边长为a的正方形ABCD剪去一个边长为b的正方形BEFG,连接DF.根据四边形ABCD,BEFG,AGFD与ECDF的面积关系.你能推出一个什么样的结论?
如图,将边长为a的正方形ABCD剪去一个边长为b的正方形BEFG,连接DF.根据四边形ABCD,BEFG,AGFD与ECDF的面积关系.你能推出一个什么样的结论? a、b在数轴上对应的点如图所示:
a、b在数轴上对应的点如图所示: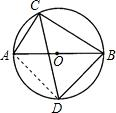 如图,AB是⊙O的直径,弦CD平分∠ACB,若AC+BC=6,则四边形ACBD的面积是
如图,AB是⊙O的直径,弦CD平分∠ACB,若AC+BC=6,则四边形ACBD的面积是