题目内容
 如图,AB是⊙O的直径,点C在AB的延长线上,AB=2BC,点D在⊙O上,∠DAO=30°.
如图,AB是⊙O的直径,点C在AB的延长线上,AB=2BC,点D在⊙O上,∠DAO=30°.(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若⊙O半径为2,求图中阴影部分的面积(结果保留π).
考点:切线的判定,扇形面积的计算
专题:
分析:(1)如图,作辅助线,证明∠ODC=90°即可解决问题;
(2)如图,作辅助线,将阴影部分分割为三角形和扇形,分别求两部分的面积问题即可解决.
(2)如图,作辅助线,将阴影部分分割为三角形和扇形,分别求两部分的面积问题即可解决.
解答: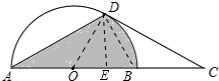 解:(1)相切.连接OD、DB,
解:(1)相切.连接OD、DB,
∵∠DAO=30°,OD=OA,
∴∠DAO=∠ADO=30°,
∴∠BOD=60°;
∵OB=OD,
∴△DOB为等边三角形,
∴OB=OD=BD,∠BDO=∠OBD=60°,
∵AB=2BC=2OB,
∴BC=OB=BD,
∴∠BDC=30°,
∴∠ODC=∠ODB+∠BDC=90°,
∴CD与⊙O相切.
(2)作DE⊥AB于点E,
∵OB=2,∠DOB=60°,
∴DE=
,
∴S阴影=S△DAO+S扇形OBD=
×2×
+
=
+
.
 解:(1)相切.连接OD、DB,
解:(1)相切.连接OD、DB,∵∠DAO=30°,OD=OA,
∴∠DAO=∠ADO=30°,
∴∠BOD=60°;
∵OB=OD,
∴△DOB为等边三角形,
∴OB=OD=BD,∠BDO=∠OBD=60°,
∵AB=2BC=2OB,
∴BC=OB=BD,
∴∠BDC=30°,
∴∠ODC=∠ODB+∠BDC=90°,
∴CD与⊙O相切.
(2)作DE⊥AB于点E,
∵OB=2,∠DOB=60°,
∴DE=
| 3 |
∴S阴影=S△DAO+S扇形OBD=
| 1 |
| 2 |
| 3 |
| 60×22π |
| 360 |
| 3 |
| 2π |
| 3 |
点评:该题以圆为载体,以切线的判定及求阴影部分的面积为为线索构造而成;解题的关键是作辅助线,灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
在△ABC和△A1B1C1中,AB=A1B1,AC=A1C1,高AD=A1D1,则∠C和∠C1的关系是( )
| A、相等 | B、互补 |
| C、相等或互补 | D、相等或互余 |
 如图,C是AB的中点,D是BC的中点,下列说法不正确的是( )
如图,C是AB的中点,D是BC的中点,下列说法不正确的是( )| A、若AC=4,则DB=2 |
| B、若CD=3,则AC=6 |
| C、若AB=8,则CD=2 |
| D、若CD=1,则AD=4 |
 在一个直角三角形铁皮上剪下一块正方形,并使正方形面积尽可能大,正方形的面积是多少?(提示:连接DB)单位:厘米.
在一个直角三角形铁皮上剪下一块正方形,并使正方形面积尽可能大,正方形的面积是多少?(提示:连接DB)单位:厘米. 已知在平行四边形ABCD中,E、F分别是边AB、AD上的点,EF与对角线AC交于点P,若
已知在平行四边形ABCD中,E、F分别是边AB、AD上的点,EF与对角线AC交于点P,若 如图所示,在△ABC中,D为BC边上的点,已知AB=13,AD=12,AC=15,BD=5,求△ACD的面积.
如图所示,在△ABC中,D为BC边上的点,已知AB=13,AD=12,AC=15,BD=5,求△ACD的面积.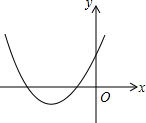 已知二次函数y=ax2+bx+c的图象如图所示,则
已知二次函数y=ax2+bx+c的图象如图所示,则