题目内容
某体育场的一条环形跑道长400米,甲、乙两人从跑道上一地点出发.分别以不同的速度练习长跑和自行车.如果背向而行,每隔30秒他们相遇一次,如果同向而行,每隔90秒甲追上乙一次,问甲、乙每分钟各行多少米?
考点:一元一次方程的应用
专题:
分析:利用题中的等量关系有:①反向而行,则两人30秒共走400米;②同向而行,则90秒乙比甲多跑400米,进而得出方程求出即可.
解答:解:∵背向而行,每隔30秒他们相遇一次,∴两人速度和为:
=
(米/分钟),
设甲的速度为x米/分钟,则乙的速度为:(
-x)米/分钟,
故90[x-(
-x)]=400,
解得;x=
,
则
-x=
-
=
(米/分钟).
答:甲每分钟行
m,乙每分钟行
m.
| 400 |
| 30 |
| 40 |
| 3 |
设甲的速度为x米/分钟,则乙的速度为:(
| 40 |
| 3 |
故90[x-(
| 40 |
| 3 |
解得;x=
| 80 |
| 9 |
则
| 40 |
| 3 |
| 120 |
| 9 |
| 80 |
| 9 |
| 40 |
| 9 |
答:甲每分钟行
| 80 |
| 9 |
| 40 |
| 9 |
点评:此题主要考查了一元一次方程的应用,根据运动的路程得出等式求出是解题关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
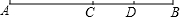 如图,C是AB的中点,D是BC的中点,下列说法不正确的是( )
如图,C是AB的中点,D是BC的中点,下列说法不正确的是( )| A、若AC=4,则DB=2 |
| B、若CD=3,则AC=6 |
| C、若AB=8,则CD=2 |
| D、若CD=1,则AD=4 |
 a、b在数轴上对应的点如图所示:
a、b在数轴上对应的点如图所示: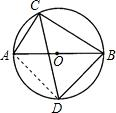 如图,AB是⊙O的直径,弦CD平分∠ACB,若AC+BC=6,则四边形ACBD的面积是
如图,AB是⊙O的直径,弦CD平分∠ACB,若AC+BC=6,则四边形ACBD的面积是