题目内容

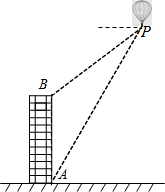如图，利用热气球探测器测量大楼AB的高度．从热气球P处测得大楼顶部B的俯角为37°，大楼底部A的俯角为60°，此时热气球P离地面的高度为120m．试求大楼AB的高度（精确到0.1m）．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，
3
≈1.73）
考点：解直角三角形的应用-仰角俯角问题
专题：
分析：首先过P作PC⊥AB，垂足为C，进而求出PC的长，利用tan37°=
BC
PC
，得BC的长，即可得出答案．
解答：解：过P作PC⊥AB，垂足为C，由已知∠APC=60°，∠BPC=37°，
且由题意可知：AC=120米．  
在Rt△APC中，由tan∠APC=
AC
PC
，
即tan60°=
120
PC
，得PC=
120
3
=40
3
．
在Rt△BPC中，由tan∠BPC=
BC
PC
，
即tan37°=
BC
PC
，得BC=40
3
×0.75≈51.9．
因此AB=AC-BC=120-51.9=68.1，
即大楼AB的高度约为68.1米．
点评：此题主要考查了解直角三角形的应用，根据题意正确构造直角三角形是解题关键．
练习册系列答案
相关题目
设a、b、c是互不相等的任意正数，x=
b2+1
a
，y=
c2+1
b
，z=
a2+1
c
，则x、y、z这三个数（　　）
A、都不大于2
B、至少有一个大于2
C、都不小于2
D、至少有一个小于2
如图，直线y1=
1
2
x+
5
2
与x轴、y轴分别交于点C、D，直线y2=3x-5与x轴、y轴分别交于点B、A，两直线交于点E．
（1）求点E的坐标；
（2）求∠CEA的度数；
（3）P（0，
9
2
）为y轴上一点，点M从点P出发以每秒1个单位的速度向点D运动，同时点Q从点D出发以每秒
5
个单位的速度向点C运动，运动时间为t，问t为何值S△EMQ的面积最大？
先化简，再求（1+
3
a2-4
）÷
1-a
a-2
的值，其中a=sin60°-2tan45°．
快、慢两车分别从相距240千米路程的甲、乙两地同时出发，匀速行驶，先相向而行，快车到达乙地后停留1小时，然后按原路原速返回，快车比慢车早1小时到达甲地，快、慢两车距甲地的路程y（千米）与出发后所用的时间x（小时）的关系如图所示．
请结合图象信息解答下列问题：
（1）快、慢两车的速度各是多少？
（2）出发多少小时，两车距甲地的路程相等？
（3）直接写出在快车到达甲地前，两车相距10千米路程的次数．
某大型物流公司首期规划建造面积为2400平方米的商铺，商铺内设A种类型和B种类型的店面共80间，A种类型的店面平均面积为28平方米，每间月租费为400元，B种类型的店面平均面积为20平方米，每间月租费为360元，全部店面的建造面积不低于商铺总面积的85%．
（1）设A种类型的店面数为a间，请问数量a在什么范围？
（2）该物流公司管理部门通过了解，A种类型的店面的出租率为75%，B种类型的店面的出租率为90%，为使店面的月租费收入最高，应建造A种类型的店面多少间？
如图，在平面直角坐标系中，正方形OABC的边长是4，点A，C分别在y轴、x轴的正半轴上，动点P从点A开始，以每秒2个单位长度的速度在线段AB上来回运动．动点Q从点B开始沿B→C→O的方向，以每秒1个单位长度的速度向点O运动．P，Q两点同时出发，当点Q到达点O时，两点同时停止运动．设运动时间为t秒．
（I）当t=1时，求PQ所在直线的解析式．
（2）当点Q在BC上运动时，若以P，B，Q为顶点的三角形与△OAP相似，求t的值．
（3）在P，Q两点运动的过程中，若△OPQ的面积为6，请直接写出所有符合条件的P点坐标．
如图，双曲线y=
k
x
（k＞0，x＞0）分别交矩形OABC的边BC、AB于E、F，交对角线OB于M，数学课时探索发现：
CE
CB
=
AF
AB
．小明思考
CE
CB
与
OM
OB
是否也存在着联系？
（1）当B（2，2）时，M是OB中点时，点E坐标是
 
； 
CE
CB
=
 
．
（2）当B（4，3）时，
OM
OB
=
1
5
，试求出
CE
CB
的值；并猜想：对于任意矩形OABC，当
OM
OB
=
1
n
时，
CE
CB
=
 
 （直接写出结果）．
（3）当
OM
OB
=
1
2
时，且∠BMF=Rt∠，求sin∠BOA的值．
已知实数a在数轴上的位置如图，则化简|1-a|+
a2
的结果为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网