题目内容
设a、b、c是互不相等的任意正数,x=
,y=
,z=
,则x、y、z这三个数( )
| b2+1 |
| a |
| c2+1 |
| b |
| a2+1 |
| c |
| A、都不大于2 |
| B、至少有一个大于2 |
| C、都不小于2 |
| D、至少有一个小于2 |
考点:反证法
专题:
分析:a、b、c是互不相等的任意正数,不妨设a>b>c>0,根据a2+b2≥2ab,即可作出判断.
解答:解:a、b、c是互不相等的任意正数,不妨设a>b>c>0,
x=
≥
=2×
,
y=
≥
=2×
,
z=
≥
=2×
.
∵a>b>c>0,
∴0<
<1,0<
<1,
>1,
∴z一定大于2,而x,y不确定.
故至少有一个大于2.
故选B.
x=
| b2+1 |
| a |
| 2b |
| a |
| b |
| a |
y=
| c2+1 |
| b |
| 2c |
| b |
| c |
| a |
z=
| a2+1 |
| c |
| 2a |
| c |
| a |
| c |
∵a>b>c>0,
∴0<
| b |
| a |
| c |
| a |
| a |
| c |
∴z一定大于2,而x,y不确定.
故至少有一个大于2.
故选B.
点评:本题考查不等式的性质,正确利用不等式的性质a2+b2≥2ab是关键.

练习册系列答案
相关题目
频数分布直方图由五个小长方形组成,且五个小长方形的高度的比是3:5:4:2:3,若第一小组频数为12,则数据总数共有( )
| A、60 | B、64 | C、68 | D、72 |
已知xa=3,xb=5,则x4a-3b=( )
| A、-44 | ||
B、
| ||
C、
| ||
D、
|
 如图,AB∥EF,∠ADC=65°,则∠CEF的度数为( )
如图,AB∥EF,∠ADC=65°,则∠CEF的度数为( )| A、25° | B、65° |
| C、135° | D、115° |
 如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1,S2,S3分别表示这三个正方形的面积,S1=81,S2=225,则S3=( )
如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1,S2,S3分别表示这三个正方形的面积,S1=81,S2=225,则S3=( ) 如图,⊙O内接△ABC,AB=AC,D是弧AC上一点,连接BD,E是BD上一点,且BE=CD.求证:∠AED=∠ADE.
如图,⊙O内接△ABC,AB=AC,D是弧AC上一点,连接BD,E是BD上一点,且BE=CD.求证:∠AED=∠ADE.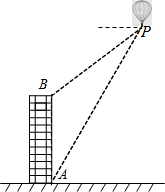 如图,利用热气球探测器测量大楼AB的高度.从热气球P处测得大楼顶部B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离地面的高度为120m.试求大楼AB的高度(精确到0.1m).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
如图,利用热气球探测器测量大楼AB的高度.从热气球P处测得大楼顶部B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离地面的高度为120m.试求大楼AB的高度(精确到0.1m).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,