题目内容
16.已知等腰梯形ABCD的上底CD等于一腰长,下底等于对角线AC的长,则等腰梯形的各个内角为∠B=72°;∠BCD=72°;∠D=108°;∠BAC=108.分析 由等腰梯形的性质可得∠DAC=∠ACD=∠ACB=$\frac{1}{2}$∠BCD,再由下底等于对角线AC的长可得∠BAD=3∠ACB,进而得到∠D=3∠ACB,由四边形内角和是360度可得10∠ACB=360°,所以梯形的各个内角即可求出.
解答 解:∵AD‖BC,
∴∠DAC=∠ACB,
∵AD=CD,
∴∠DAC=∠ACD,
∴∠DAC=∠ACD=∠ACB=$\frac{1}{2}$∠BCD,
∵AC=BC,
∴∠B=∠BAC,
∵四边形ABCD等腰梯形,
∴∠B=∠BCD,
∴∠B=2∠ACB,
∵∠DAC+∠BAC=∠BAD,
∴∠BAD=3∠ACB,
∴∠BAD=∠D,
∴∠D=3∠ACB,
∴10∠ACB=360°,
∴∠B=72°;∠BCD=72°;∠D=108°;∠BAC=108°,
故答案为∠B=72°;∠BCD=72°;∠D=108°;∠BAC=108.
点评 本题考查了等腰梯形的性质以及四边形的内角和定理的运用,解题的关键是利用已知条件得到各个内角和∠ACB的数量关系,再由四边形的内角和定理得出10∠ACB=360°.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
1.下面是某商场电脑产品的进货单,其中标价一栏被烧掉,请根据其他栏内的信息求出标价.
| 进价 | 标价 | 折扣 | 利润 |
| 3000 | 八折 | 200 |
5.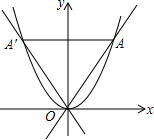 如图所示,直线y=2x和y=-2x分别与抛物线y=x2交于点O,A和点0,A′,则下列说法中错误的是( )
如图所示,直线y=2x和y=-2x分别与抛物线y=x2交于点O,A和点0,A′,则下列说法中错误的是( )
 如图所示,直线y=2x和y=-2x分别与抛物线y=x2交于点O,A和点0,A′,则下列说法中错误的是( )
如图所示,直线y=2x和y=-2x分别与抛物线y=x2交于点O,A和点0,A′,则下列说法中错误的是( )| A. | 点A′和点A关于y轴对称 | |
| B. | △AOA′是等腰三角形 | |
| C. | S△AOA′=8 | |
| D. | 线段OA绕点O逆时针旋转60°可与线段OA′重合 |
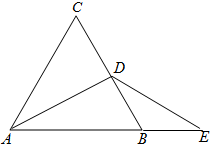 如图,在等边三角形ABC中,D是BC边的中点,E是AB延长线上的一点,且BE=BD.
如图,在等边三角形ABC中,D是BC边的中点,E是AB延长线上的一点,且BE=BD. 已知如图:平面直角坐标系中,A(3,0),B(0,3),AD平分∠BAO.BD⊥AD于D.并连DO,求∠ADO的大小?
已知如图:平面直角坐标系中,A(3,0),B(0,3),AD平分∠BAO.BD⊥AD于D.并连DO,求∠ADO的大小? 如图.已知P为∠ABC平分线上的一点,且PE=PF,结合所学知识,
如图.已知P为∠ABC平分线上的一点,且PE=PF,结合所学知识, 如图,在锐角△ABC中,已知AB=15,BC=14,AC=13,AD⊥BC于D点,求AD的长.
如图,在锐角△ABC中,已知AB=15,BC=14,AC=13,AD⊥BC于D点,求AD的长.