题目内容
14.如图1,若顺次连接四边形ABCD各边中点多的四边形EFGH是矩形,则称原四边形ABCD为“中母矩形”即若四边形的对角线互相垂直,那么这个四边形称为“中母矩形”.(1)如图2,在直角坐标系xOy中,已知A(4,0),B(1,4),C(4,6),请在格点上标出D点的位置(只标一点即可),使四边形ABCD是中母矩形.并写出点D的坐标.
(2)如图3,以△ABC的边AB,AC为边,向三角形外作正方形ABDE及ACFG,连接CE,BG相交于点O,试判断四边形BEGC是中母矩形?说明理由.
(3)如图4,在Rt△ABC中,AB=8,BC=6,E是斜边AC的中点,F是直角边AB的中点,P是直角边BC上一动点,试探究:当P在BC边上什么位置时,四边形BPEF是中母矩形?
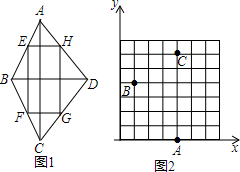

分析 (1)根据中母矩形的定义进而得出当BD∥x轴时,D在线段AC右侧即可;
(2)利用正方形的性质结合全等三角形的判定方法得出△EAC≌△GAB(SAS),进而得出EC⊥BG,得出答案即可;
(3)利用中母矩形的定义结合相似三角形的性质与判定得出BP的长即可.
解答  解:(1)如图2所示:点D即为所求,D(6,4);
解:(1)如图2所示:点D即为所求,D(6,4);
(2)如图3,∵正方形ABDE及ACFG,
∴∠EAB=∠GAC=90°,AG=AC,AE=AB,
∴∠EAC=∠EAB+∠BAC=∠GAB=∠GAC+∠BAC,
在△EAC和△GAB中
∵$\left\{\begin{array}{l}{GA=AC}\\{∠EAC=∠GAB}\\{AE=AB}\end{array}\right.$,
∴△EAC≌△GAB(SAS),
∴∠ABG=∠AEC,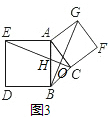
∴∠AEC+∠AHE=∠ABG+∠BHO=90°,
∴EC⊥BG,
∴四边形BEGC是中母矩形;
(3)如图4,
当△BFE∽△PBF时,则∠FPB=∠FBE,
∵∠BFP+∠BPF=90°,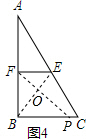
∴∠EBF+∠BFP=90°,
∴FP⊥BE,
即此时$\frac{EF}{BF}$=$\frac{BF}{BP}$,
∵AB=8,BC=6,E是斜边AC的中点,F是直角边AB的中点,
∴BF=4,EF=3,
∴BP=$\frac{16}{3}$,
即当P在BC边上,BP=$\frac{16}{3}$时,四边形BPEF是中母矩形.
点评 此题主要考查了四边形综合以及相似三角形的判定与性质、全等三角形的判定与性质等知识,正确把握中母矩形的定义是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.将14 900 000用科学记数法表示是( )
| A. | 1.49×106 | B. | 0.149×108 | C. | 1.49×107 | D. | 14.9×107 |
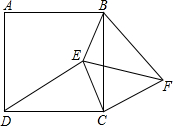 如图,四边形ABCD是正方形,E是正方形ABCD内一点,F是正方形ABCD外一点,连结BE、CE、DE、BF、CF、EF.
如图,四边形ABCD是正方形,E是正方形ABCD内一点,F是正方形ABCD外一点,连结BE、CE、DE、BF、CF、EF.