题目内容
5．先化简，再求值：（$\frac{1}{x+y}$-$\frac{1}{x-y}$）÷$\frac{2y}{{x}^{2}-2xy{+y}^{2}}$，其中x=$\sqrt{3}$+$\sqrt{2}$，y=$\sqrt{3}$-$\sqrt{2}$．
分析 原式括号中两项通分并利用同分母分式的加法法则计算，同时利用除法法则变形，约分得到最简结果，将x=$\sqrt{3}$+$\sqrt{2}$，y=$\sqrt{3}$-$\sqrt{2}$代入计算即可求出值．
解答 解：原式=$\frac{-2y}{（x+y）（x-y）}$•$\frac{（x-y）^{2}}{2y}$=-$\frac{x-y}{x+y}$，
当x=$\sqrt{3}$+$\sqrt{2}$，y=$\sqrt{3}$-$\sqrt{2}$时，原式=-$\frac{\sqrt{3}+\sqrt{2}-\sqrt{3}+\sqrt{2}}{\sqrt{3}+\sqrt{2}+\sqrt{3}-\sqrt{2}}$=-$\frac{\sqrt{6}}{3}$．
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
华东师大版一课一练系列答案
相关题目
15．
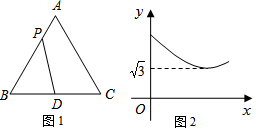如图1，在等边△ABC中，点D是BC边的中点，点P为AB 边上的一个动点，设AP=x，PD=y，若y与x之间的函数关系的图象如图2所示，则等边△ABC的面积为（ ）
如图1，在等边△ABC中，点D是BC边的中点，点P为AB 边上的一个动点，设AP=x，PD=y，若y与x之间的函数关系的图象如图2所示，则等边△ABC的面积为（ ）| A． | 4 | B． | $2\sqrt{3}$ | C． | 12 | D． | $4\sqrt{3}$ |
如图，已知OC是∠AOB的平分线，P是OC上一点，PD⊥OA于点D，PD=2，则点P到OB的距离为2．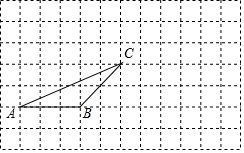
（1）过点A画出BC的平行线；
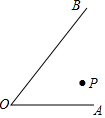如图所示，在∠AOB内有一点P．
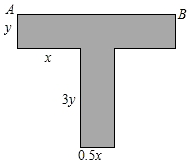某种T型零件尺寸如图所示（左右宽度相同），求：