题目内容
12.在△ABC中,∠B=45°,∠C=60°.(1)如图1,若AB=5$\sqrt{2}$,求BC的长;
(2)点D是CB边的延长线上一点,连接AD,将线段AD绕点A逆时针旋转90°,得到线段AE,如图2,当点E恰在AC边上时,计算CE与BD的关系数量.

分析 (1)在Rt△ABD中,求出AD、BD,再在Rt△ADC中求出CD即可解决问题.
(2)结论:CE=($\sqrt{3}$-1)BD.如图2中,作AF⊥BC于F,设AC=a.想办法用a表示线段BD,CE即可解决问题.
解答 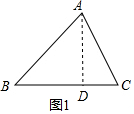 解:(1)如图1,过A作AD⊥BC于D,
解:(1)如图1,过A作AD⊥BC于D,
∴∠ADB=∠ADC=90°,
∵∠B=45°,
∴AD=BD=$\frac{\sqrt{2}}{2}$AB=5,
∵∠C=60°,
∴CD=$\frac{\sqrt{3}}{3}$AD=$\frac{5\sqrt{3}}{3}$,
∴BC=BD+CD=5$+\frac{5\sqrt{3}}{3}$;
(2)结论:CE=($\sqrt{3}$-1)BD.
理由:如图2中,作AF⊥BC于F,设AC=a.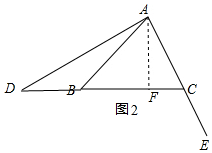
在Rt△ADC中,∵∠DAC=90°,∠D=30°,
∴DC=2a,AD=AE=$\sqrt{3}$a,
在Rt△AFC中,∵∠FAC=90°,∠FAC=30°,
∴CF=$\frac{1}{2}$AC=$\frac{1}{2}$a,AF=$\frac{\sqrt{3}}{2}$a,
在Rt△ABF中,∵∠ABF=∠BAF=45°,
∴BF=AF=$\frac{\sqrt{3}}{2}$a,
∴DB=CD-BF-CF=a,
∵CE=AE-AC=($\sqrt{3}$-1)a,
∴CE=($\sqrt{3}$-1)BD.
点评 本题考查旋转变换、解直角三角直角三角形30°角性质等知识,解题的关键是记住30°的直角三角形的三边之比为1:$\sqrt{3}$:2,45°是直角三角形的三边之比为1:1:$\sqrt{2}$,属于中考常考题型.

练习册系列答案
相关题目
2.下列计算错误的是( )
| A. | $\frac{{a}^{3}{b}^{2}}{{a}^{2}{b}^{3}}$=$\frac{a}{b}$ | B. | $\frac{(a-b)^{2}}{b-a}$=a-b | ||
| C. | $\frac{{m}^{2}-2m}{4-{m}^{2}}$=-$\frac{m}{m+2}$ | D. | $\frac{0.2a+b}{0.5a-b}$=$\frac{2a+10b}{5a-10b}$ |
17.如图所示,数轴的单位长度为1,如果点M、N表示的数的绝对值相等,那么点M表示的数是( )


| A. | -4 | B. | -3 | C. | -2 | D. | 3 |
16.已知平面内有A,B,C,D四点,过其中的两点画一条直线,一共可以画( )直线.
| A. | 1条 | B. | 4条 | C. | 6条 | D. | 1条、4条或6条 |
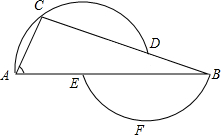 如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,已知∠A=66°,试求∠B的度数.
如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,已知∠A=66°,试求∠B的度数.
 如图,点D、E、F分别为△ABC的三边中点,试说明△ABC∽△EFD.
如图,点D、E、F分别为△ABC的三边中点,试说明△ABC∽△EFD.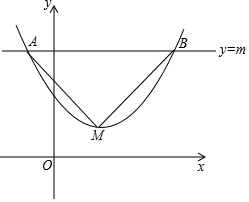 抛物线y=a(x-2)2+3(a>0),直线y=m交抛物线于A、B两点,M为顶点,△ABM为直角三角形,求AB的长.
抛物线y=a(x-2)2+3(a>0),直线y=m交抛物线于A、B两点,M为顶点,△ABM为直角三角形,求AB的长.