题目内容
3.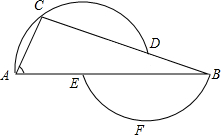 如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,已知∠A=66°,试求∠B的度数.
如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,已知∠A=66°,试求∠B的度数.
分析 连接CE、DE.首先证明∠CED=180°-∠DCE-∠CDE=180°-2∠DBE-2∠DBE=180°-4∠DBE,再根据∠CED+∠DEB=∠CEB=132°,可得180°-4∠DBE+∠DBE=132°,即可解决问题.
解答 解:连接CE、DE.
∵AE=CE,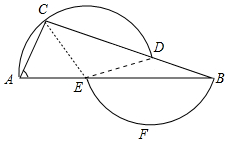
∴∠A=∠ACE=66°,
∴∠CEB=∠A+∠ACE=132°,
∵DE=BD,
∴∠DBEB=∠DEB,
∴∠CDE=∠DEB+∠DBE=2∠DBE,
∵CE=DE,
∴∠EDC=∠ECD=2∠DBE,
∴∠CED=180°-∠DCE-∠CDE=180°-2∠DBE-2∠DBE=180°-4∠DBE,
∵∠CED+∠DEB=∠CEB=132°,
∴180°-4∠DBE+∠DBE=132°,
∴∠DBE=16°.
点评 本题考查圆周角定理、半径的性质、等腰直角三角形的性质、三角形的外角的性质等知识,解题的关键是学会利用方程的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目

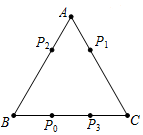 如图,电子跳蚤游戏盘是如图所示的△ABC,AB=BC=AC=6.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2012与点P2013之间的距离为( )
如图,电子跳蚤游戏盘是如图所示的△ABC,AB=BC=AC=6.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2012与点P2013之间的距离为( )