题目内容
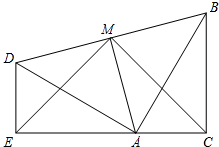 两个全等的含有30°,60°角的三角尺ADE与三角尺ABC如图所示放置,E,A,C三点在一条直线上,连接BD,取BD的中点M,连接ME,MC.
两个全等的含有30°,60°角的三角尺ADE与三角尺ABC如图所示放置,E,A,C三点在一条直线上,连接BD,取BD的中点M,连接ME,MC.(1)求证:△EDM≌△CAM;
(2)求证:△EMC为等腰直角三角形.
考点:全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:(1)易证△ABD是等腰直角三角形,根据等腰三角形的三线合一,得出AM⊥BD,得出∴∠DAM=∠MAB=∠ABM=∠ADM=45°,DM=MA=MB,进而求得∠EDM=∠MAC,然后根据SAS即可求得结论;
(2)根据△EDM≌△CAM,得出∠EMD=∠AMC,EM=CM,根据∠AMD=∠EMD+∠AME=90°,推出∠EMC=∠AMC+∠AME=90°,即可证得:△EMC为等腰直角三角形
(2)根据△EDM≌△CAM,得出∠EMD=∠AMC,EM=CM,根据∠AMD=∠EMD+∠AME=90°,推出∠EMC=∠AMC+∠AME=90°,即可证得:△EMC为等腰直角三角形
解答:解:(1)∵AB=AD,
∴△ABD是等腰三角形,
∵∠DAE=30°,∠BAC=60°,
∴∠DAB=90°
∴三角形ABD是等腰直角三角形,
∵DM=BM,
∴AM⊥BD,
∴∠DAM=∠MAB=∠ABM=∠ADM=45°,DM=MA=MB,
∵∠ADE=∠BAC=60°,
∴∠EDM=∠MAC=60°+45°,
在△EDM与△CAM中
∴△EDM≌△CAM(SAS);
(2)∵△EDM≌△CAM,
∴∠EMD=∠AMC,EM=CM,
∵∠AMD=∠EMD+∠AME=90°,
∴∠EMC=∠AMC+∠AME=90°,
∴△EMC是等腰直角三角形,
∴△ABD是等腰三角形,
∵∠DAE=30°,∠BAC=60°,
∴∠DAB=90°
∴三角形ABD是等腰直角三角形,
∵DM=BM,
∴AM⊥BD,
∴∠DAM=∠MAB=∠ABM=∠ADM=45°,DM=MA=MB,
∵∠ADE=∠BAC=60°,
∴∠EDM=∠MAC=60°+45°,
在△EDM与△CAM中
|
∴△EDM≌△CAM(SAS);
(2)∵△EDM≌△CAM,
∴∠EMD=∠AMC,EM=CM,
∵∠AMD=∠EMD+∠AME=90°,
∴∠EMC=∠AMC+∠AME=90°,
∴△EMC是等腰直角三角形,
点评:本题考查了等腰直角三角形,全等三角形的性质和判定,主要考查学生综合运用性质进行推理的能力,题目比较典型,但是有一定的难度.

练习册系列答案
相关题目
 如图所示,∠A=∠C,求证:∠ADB=∠CEB.
如图所示,∠A=∠C,求证:∠ADB=∠CEB.