题目内容
已知1、2、3、4、5、6、7标准差为2,则101、202、303、404、505、606、707的标准差为 .
考点:标准差
专题:
分析:先求出101、202、303、404、505、606、707的平均数,再根据方差公式求出101、202、303、404、505、606、707的方差,最后根据标准差即可得出答案.
解答:解:∵101、202、303、404、505、606、707的平均数是404,
∴101、202、303、404、505、606、707的方差=
[(101-404)2+(202-404)2+(303-404)2+(404-404)2+(505-404)2+(606-404)2+(707-404)2]
=40804,
∴101、202、303、404、505、606、707的标准差为
=202;
故答案为:202.
∴101、202、303、404、505、606、707的方差=
| 1 |
| 7 |
=40804,
∴101、202、303、404、505、606、707的标准差为
| 40804 |
故答案为:202.
点评:本题考查了方差和标准差:一般地设n个数据,x1,x2,…xn的平均数为
,则方差S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
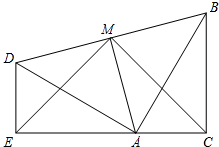 两个全等的含有30°,60°角的三角尺ADE与三角尺ABC如图所示放置,E,A,C三点在一条直线上,连接BD,取BD的中点M,连接ME,MC.
两个全等的含有30°,60°角的三角尺ADE与三角尺ABC如图所示放置,E,A,C三点在一条直线上,连接BD,取BD的中点M,连接ME,MC. 如图,A、B、C是⊙O上三点,若∠OAB=44°,则∠ACB=
如图,A、B、C是⊙O上三点,若∠OAB=44°,则∠ACB=