题目内容
如果方程x2+ax+b=0的两个根分别是-1+
和-1-
,求a,b的值.
| 3 |
| 3 |
考点:根与系数的关系
专题:
分析:根据x1+x2=-
,x1•x2=
得出方程,求出即可.
| b |
| a |
| c |
| a |
解答:解:∵x2+ax+b=0的两个根分别是-1+
和-1-
,
∴-1+
+(-1-
)=-a,(-1+
)×(-1-
)=b,
解得:a=2,b=-2.
| 3 |
| 3 |
∴-1+
| 3 |
| 3 |
| 3 |
| 3 |
解得:a=2,b=-2.
点评:此题主要考查了一元二次方程根与系数的关系,根据题意得出x1+x2=-
和x1•x2=
的值是解决问题的关键.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
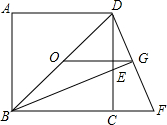 如图,O是正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.
如图,O是正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG. 如图所示,△ABC中,DE∥BC且DE:BC=2:3,若S△ADE=9,求S四边形DBCE.
如图所示,△ABC中,DE∥BC且DE:BC=2:3,若S△ADE=9,求S四边形DBCE.
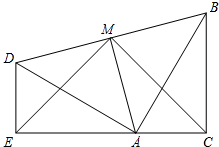 两个全等的含有30°,60°角的三角尺ADE与三角尺ABC如图所示放置,E,A,C三点在一条直线上,连接BD,取BD的中点M,连接ME,MC.
两个全等的含有30°,60°角的三角尺ADE与三角尺ABC如图所示放置,E,A,C三点在一条直线上,连接BD,取BD的中点M,连接ME,MC.