题目内容
观察下面图形,解答下列问题:
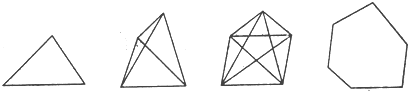
(1)观察规律,把下表填写完整:
(2)若一个多边形的内角和为1440°,求这个多边形的边数和对角线的条数.

(1)观察规律,把下表填写完整:
| 边数 | 三 | 四 | 五 | 六 | 七 | … | n |
| 对角线条数 | 0 | 2 | 5 | … |
考点:多边形内角与外角,规律型:图形的变化类,多边形的对角线
专题:
分析:(1)过n边形的一个顶点可画出(n-3)条对角线,那么过n个顶点可以画出n(n-3)条对角线,根据两点确定一条直线,再把所得结果除以2即可求得多边形的对角线的总条数;
(2)根据内角和公式可得多边形的边数,把边数代入(1)得到的公式即可求得相应的对角线条数.
(2)根据内角和公式可得多边形的边数,把边数代入(1)得到的公式即可求得相应的对角线条数.
解答:解:(1)
(2)设多边形的边数为n.
则(n-2)×180=1440,
解得n=10.
∴对角线的条数为:
=35(条).
故答案为9,14,
.
| 边数 | 三 | 四 | 五 | 六 | 七 | … | n | ||
| 对角线条数 | 0 | 2 | 5 | 9 | 14 | … |
|
则(n-2)×180=1440,
解得n=10.
∴对角线的条数为:
| 10(10-3) |
| 2 |
故答案为9,14,
| n(n-3) |
| 2 |
点评:主要考查三角形的内角和公式及n边形对角线的条数的规律.根据一个顶点处的对角线条数得到n边形对角线的条数的相应规律是解决本题的难点.

练习册系列答案
相关题目
若9a2+6(k-3)a+1是完全平方式,则k的值是( )
| A、±4 | B、±2 | C、3 | D、4或2 |
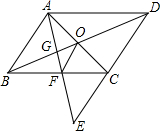 点E为平行四边形ABCD中DC边的延长线上的一点,且CE=DC,连接AE分别交BC、BD于点F、G,连接AC交BD于点O,连接OF.
点E为平行四边形ABCD中DC边的延长线上的一点,且CE=DC,连接AE分别交BC、BD于点F、G,连接AC交BD于点O,连接OF. 周末,小明骑自行车从家里出发到野外郊游,从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(千米)与小明离家时间x(小时)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
周末,小明骑自行车从家里出发到野外郊游,从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(千米)与小明离家时间x(小时)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.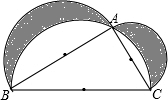 如图,分别以直角三角形两直角边AB、AC及斜边BC为直径向外作半圆(以BC为直径的半圆过点A),∠BAC=90°,AB=4cm,AC=3cm,BC=5cm.求图中阴影部分的面积.
如图,分别以直角三角形两直角边AB、AC及斜边BC为直径向外作半圆(以BC为直径的半圆过点A),∠BAC=90°,AB=4cm,AC=3cm,BC=5cm.求图中阴影部分的面积.
 如图,AB∥CD,∠1=(3x+50)°,∠2=(2x+30)°,则∠3的度数为
如图,AB∥CD,∠1=(3x+50)°,∠2=(2x+30)°,则∠3的度数为