题目内容
11.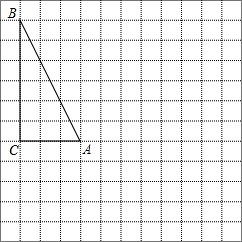 在如图所示的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=6.
在如图所示的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=6.(1)试作出△ABC以A为旋转中心、沿顺时针方向旋转90°后的图形△AB1C1;
(2)求点B旋转到点B1所经过的路线长.
分析 (1)直接利用旋转的性质得出对应点位置进而得出答案;
(2)利用勾股定理得出AB的长,再利用弧长公式求出答案.
解答  解:(1)如图所示:△AB1C1,即为所求;
解:(1)如图所示:△AB1C1,即为所求;
(2)∵AB=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$,
∴点B旋转到点B1所经过的路线长为:l=$\frac{90π×3\sqrt{5}}{180}$=$\frac{3\sqrt{5}}{2}$π.
点评 此题主要考查了旋转变换以及弧长公式的应用,正确记忆弧长公式是解题关键.

练习册系列答案
相关题目
6. 二次函数y=ax2+bx+c的图象如图所示,则下列关系式不正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列关系式不正确的是( )
 二次函数y=ax2+bx+c的图象如图所示,则下列关系式不正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列关系式不正确的是( )| A. | a<0 | B. | c>0 | C. | b2-4ac>0 | D. | b>0 |
3.下列命题中,
①长为5cm的线段AB沿某一方向平移10cm后,平移后线段AB的长为10cm
②三角形的高在三角形内部
③六边形的内角和是外角和的两倍
④平行于同一直线的两条直线平行
⑤两个角的两边分别平行,则这两个角相等.
真命题个数有( )
①长为5cm的线段AB沿某一方向平移10cm后,平移后线段AB的长为10cm
②三角形的高在三角形内部
③六边形的内角和是外角和的两倍
④平行于同一直线的两条直线平行
⑤两个角的两边分别平行,则这两个角相等.
真命题个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.下列运算正确的是( )
| A. | a3-a2=a | B. | a2•a3=a6 | C. | (-3a)3=-9a3 | D. | (-a3)2=a6 |
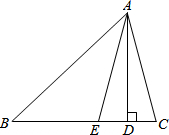 如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=45°,∠C=75°,求∠DAE的度数.
如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=45°,∠C=75°,求∠DAE的度数.