Question

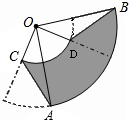如图，扇形OAB与扇形OCD的圆心角都是90°，连结AC，BD．
（1）求证：AC=BD；
（2）若图中阴影部分的面积是

7

4

πcm2，OC=3cm，求OA的长．

Answer 1

考点：扇形面积的计算,全等三角形的判定与性质

专题：计算题

分析：（1）根据等角的余角相等得∠AOC=∠BOD，则可根据“SAS”证明△AOC≌△AOD，则AC=BD；
（2）如图，由于∠COF=∠EOD，则S_扇形COF=S_扇形EOD，加上S_△AOC=S_△AOD，易得S=S′，于是S_阴影部分=S_扇形AOB-S_扇形EOF，然后根据扇形面积公式得

90•π•OA2

360

-

90•π•32

360

=

7

4

π，然后解方程即可求出OA．

解答：（1）证明：∵∠COD=∠AOB=90°，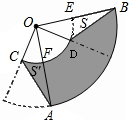
即∠AOC+∠AOD=∠BOD+∠AOD，
∴∠AOC=∠BOD，
在△AOC和△BOD中，

AO=BO ∠AOC=∠BOD CO=DO

，
∴△AOC≌△AOD，
∴AC=BD；
（2）解：如图，∵∠COF=∠EOD，
∴S_扇形COF=S_扇形EOD，
而S_△AOC=S_△AOD，
∴S=S′，
∴S_阴影部分=S_扇形AOB-S_扇形EOF，
∴

90•π•OA2

360

-

90•π•32

360

=

7

4

π，
∴OA=4（cm）．

点评：本题考查了扇形面积的计算：设圆心角是n°，圆的半径为R的扇形面积为S，则S_扇形=

360

n

πR²或S_扇形=

1

2

lR（其中l为扇形的弧长．也考查了利用面积的和差计算不规则图形的面积．