题目内容
用含30°、45°、60°这三个特殊角的四个三角比及其组合可以表示某些实数,如:
可表示为
=sin30°=cos60°=tan45°•sin30°=…;仿照上述材料,完成下列问题:
(1)用含30°、45°、60°这三个特殊角的三角比或其组合表示
,即填空:
= = =…;
(2)用含30°、45°、60°这三个特殊角的三角比,结合加、减、乘、除四种运算,设计一个等式,要求:等式中须含有这三个特殊角的三角比,上述四种运算都至少出现一次,且这个等式的结果等于1,即填空:1= .
| 1 |
| 2 |
| 1 |
| 2 |
(1)用含30°、45°、60°这三个特殊角的三角比或其组合表示
| ||
| 2 |
| ||
| 2 |
(2)用含30°、45°、60°这三个特殊角的三角比,结合加、减、乘、除四种运算,设计一个等式,要求:等式中须含有这三个特殊角的三角比,上述四种运算都至少出现一次,且这个等式的结果等于1,即填空:1=
考点:特殊角的三角函数值
专题:
分析:(1)根据30°、45°、60°这三个特殊角的三角比进行填空;
(2)因为该等式的要求是:等式中须含有这三个特殊角的三角比,上述四种运算都至少出现一次,且这个等式的结果等于1,所以首先考虑到tan45°=cot45°=1.
(2)因为该等式的要求是:等式中须含有这三个特殊角的三角比,上述四种运算都至少出现一次,且这个等式的结果等于1,所以首先考虑到tan45°=cot45°=1.
解答:解:(1)∵sin60°=cos30°=
,tan45°=1,
∴
=sin60°=cos30°=tan45°•sin60°=…;
故答案是:=sin60°;cos30°;tan45°•sin60°;
(2)∵
=sin30°=cos60°,tan45°=cot45°=1.
∴该等式可以是1=(sin30°+cos60°)•tan45°÷cot45°.
故答案是:(sin30°+cos60°)•tan45°÷cot45°(答案不唯一).
| ||
| 2 |
∴
| ||
| 2 |
故答案是:=sin60°;cos30°;tan45°•sin60°;
(2)∵
| 1 |
| 2 |
∴该等式可以是1=(sin30°+cos60°)•tan45°÷cot45°.
故答案是:(sin30°+cos60°)•tan45°÷cot45°(答案不唯一).
点评:本题考查了特殊角的三角函数值.解决此类题目的关键是熟记特殊角的三角函数值.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
计算:(2+1)(22+1)(24+1)(28+1)的值为( )
| A、48-1 |
| B、264-1 |
| C、26-1 |
| D、23-1 |
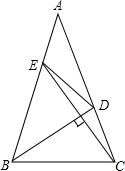 如图,△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,CE⊥BD交于E,连接DE,则图中等腰三角形有( )
如图,△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,CE⊥BD交于E,连接DE,则图中等腰三角形有( )| A、3个 | B、4个 | C、5个 | D、6个 |
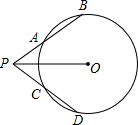 已知:如图,⊙O的半径为5,P为⊙O外一点,PB、PD与⊙O分别交于点A、B和点C、D,且PO平分∠BPD.
已知:如图,⊙O的半径为5,P为⊙O外一点,PB、PD与⊙O分别交于点A、B和点C、D,且PO平分∠BPD.
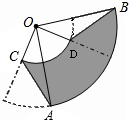 如图,扇形OAB与扇形OCD的圆心角都是90°,连结AC,BD.
如图,扇形OAB与扇形OCD的圆心角都是90°,连结AC,BD.