题目内容
16.化简:$\frac{{2\sqrt{10}}}{{\sqrt{7}-\sqrt{2}+\sqrt{5}}}$.分析 把分子部分利用完全平方公式和平方差公式变形,然后约分即可.
解答 解:原式=$\frac{7-(\sqrt{5}-\sqrt{2})^{2}}{\sqrt{7}-\sqrt{2}+\sqrt{5}}$
=$\frac{(\sqrt{7}+\sqrt{5}-\sqrt{2})(\sqrt{7}-\sqrt{5}+\sqrt{2})}{\sqrt{7}-\sqrt{2}+\sqrt{5}}$
=$\sqrt{7}$-$\sqrt{5}$+$\sqrt{2}$.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
4. 点A、B、C、D都在如图所示的由正方形组成的网格图中,且线段CD与线段AB成位似图形,则位似中心为( )
点A、B、C、D都在如图所示的由正方形组成的网格图中,且线段CD与线段AB成位似图形,则位似中心为( )
 点A、B、C、D都在如图所示的由正方形组成的网格图中,且线段CD与线段AB成位似图形,则位似中心为( )
点A、B、C、D都在如图所示的由正方形组成的网格图中,且线段CD与线段AB成位似图形,则位似中心为( )| A. | 点E | B. | 点F | C. | 点H | D. | 点G |
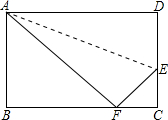 如图所示,沿AE折叠长方形ABCD使点D恰好落在BC边上的点F处.已知AB=8cm,BC=10cm.
如图所示,沿AE折叠长方形ABCD使点D恰好落在BC边上的点F处.已知AB=8cm,BC=10cm.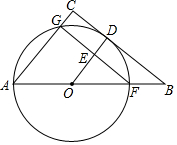 如图,在△ABC中,F是AB上一点,以AF为直径的⊙O切BC于点D,交AC于点G,AC∥OD,OD与GF交于点E.
如图,在△ABC中,F是AB上一点,以AF为直径的⊙O切BC于点D,交AC于点G,AC∥OD,OD与GF交于点E.