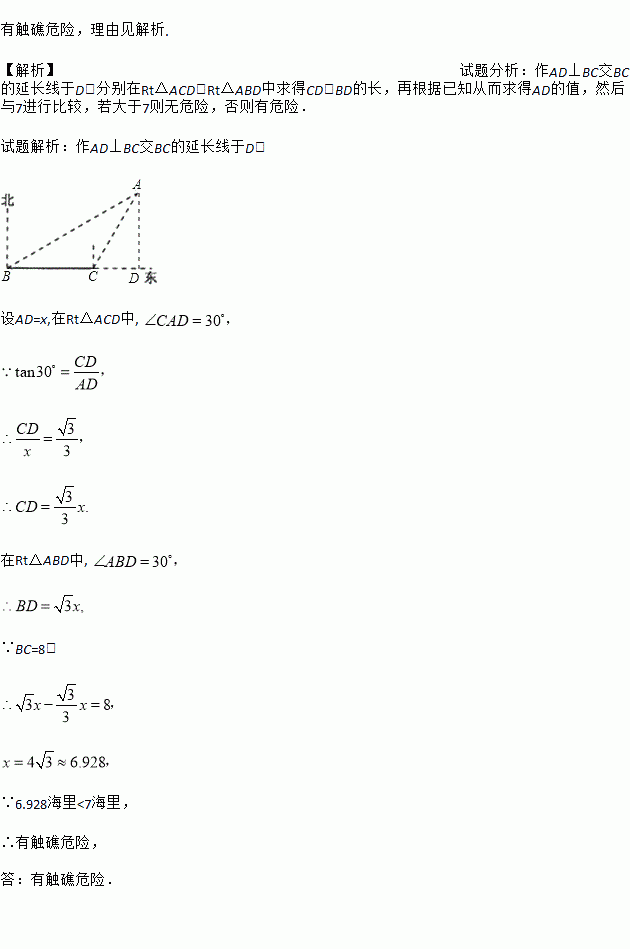题目内容
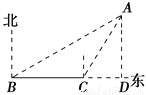
如图，已知灯塔A的周围7海里的范围内有暗礁，一艘渔轮在B处测得灯塔A在北偏东60°的方向，向正东航行8海里到C处后，又测得该灯塔在北偏东30°方向，渔轮不改变航向，继续向东航行，有没有触礁危险？请通过计算说明理由．(参考数据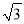
≈1.732)
有触礁危险，理由见解析.
【解析】试题分析：作AD⊥BC交BC的延长线于D，分别在Rt△ACD，Rt△ABD中求得CD、BD的长，再根据已知从而求得AD的值，然后与7进行比较，若大于7则无危险，否则有危险．
试题解析：作AD⊥BC交BC的延长线于D，
设AD=x,在Rt△ACD中,
在Rt△ABD中,
∵BC=8，
∵6.928海里<7海里，
∴有触礁危险...
练习册系列答案
相关题目
直角坐标系中，已知点P(－2，－1)，点T(t，0)是x轴上的一个动点.
(1)求点P关于原点的对称点P′的坐标;
(2)当t取何值时，△P′TO是等腰三角形?
（1）点P关于原点的对称点P′的坐标为(2，1)；（2）综上所述，符合条件的t的值为－， ， ，4.
【解析】试题分析: （1）根据坐标关于原点对称的特点即可得出点P′的坐标,（2）要分类讨论,动点T在原点左侧和右侧时分别进行讨论即可得出当t取何值时,△P′TO是等腰三角形.
试题解析:(1) 点P关于原点的对称点P′的坐标为(2,1).
(2)OP′=.
(a)动点T在原... 下面说法错误的是 ( )
A. 三角形的三条角平分线交于一点 B. 三角形的三条中线交于一点
C. 三角形的三条高交于一点 D. 三角形的三条高所在的直线交于一点
C
【解析】A. 三角形的三条角平分线交于一点，是三角形的内心，故命题正确；
B. 三角形的三条中线交于一点，是三角形的重心，故命题正确；
三角形的三条高所在的直线交于一点，三条高不一定相交，故C错误，D正确。
故选C. 如图,已知△ABC和△BDE均为等边三角形.试说明:BD+CD=AD.
见解析
【解析】首先证明△ABE≌△CBD，进而得到DC=AE，再由AD=AE+ED利用等量代换即可证出AD=BD+CD．
证明：因为△ABC,△BDE均为等边三角形,
所以BE=BD=DE,AB=BC,∠ABC=∠EBD=60°.
所以∠ABE+∠EBC=∠DBC+∠EBC.
所以∠ABE=∠DBC.
在△ABE和△CBD中,
所以△ABE≌△CBD(S... 如图,图案⑥是由图①~⑤中五种基本图形中的两种拼接而成的,则这两种基本图形是( )
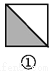
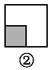
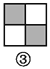
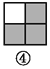
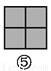
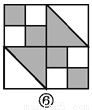
A. ①② B. ①③ C. ①④ D. ③⑤
B
【解析】根据已知图形，利用分割与组合的原理对图形进行分析即可．
【解析】
如图所示：图案⑥是由图①和图③这两种基本图形拼接而成的.
故选：B. 如图，已知tan O＝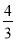
，点P在边OA上，OP＝5，点M，N在边OB上，PM＝PN，如果MN＝2，那么PM＝________．
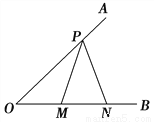
【解析】试题解析：过P作PD⊥OB，交OB于点D，
∴设PD=4x，则OD=3x，
∵OP=5,由勾股定理得：
∴x=1，
∴PD=4，
∵PM=PN，PD⊥OB，MN=2
在Rt△PMD中，由勾股定理得：
故答案为： 在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，下列等式中不一定成立的是（ ）
A. b=atanB B. a=ccosB C. c＝
D. a=bcosA
D
【解析】∵∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，
∴A.tanB= ，则b=atanB，故本选项正确，
B.cosB= ，故本选项正确，
C.sinA= ，故本选项正确，
D.cosA= ，故本选项错误，
故选D． 当角度在0°到90°之间变化时，函数值随着角度的增大而增大的三角函数是（ ）
A. 正弦和余弦 B. 正弦和正切 C. 余弦和正切 D. 正弦、余弦和正切
B
【解析】当角度在0°到90°之间变化时，函数值随着角度的增大而增大的三角函数是正弦和正切．
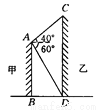
故选B． 如图所示，两建筑物的水平距离为24 m，从A点测得D点的俯角为60°，测得C点的仰角为40°，求这两座建筑物的高．(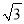
≈1.732，tan 40°≈0.8391，精确到0.01 m)
61.7l m
【解析】试题分析：过点A作AE⊥CD于点E，可得四边形ABDE为矩形，AB=ED，BD=AE，然后在Rt△AED和Rt△AEC中，分别求出DE和EC的长度，继而可求得建筑物CD的高度和建筑物AB的高度．
试题解析：作AE⊥CD于E，
则AE=BD=24m，
在Rt△AED中，tan∠DAE=，
∴DE=AEtan 60°≈24×1.732≈41.57(...