题目内容
比较下列三角函数值的大小：sin40°______cos40°（选填“＞”、“=”、“＜”）
【解析】∵cos40°=sin50°，正弦值随着角的增大而增大，
又∵40°＜50°，
∴sin40°＜cos40°
练习册系列答案
相关题目
如图，该五角星中，∠A＋∠B＋∠C＋∠D＋∠E=________度．
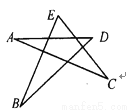
180°
【解析】试题解析：如图所示：
∵∠DGE是△EGB的外角，∴∠DGF=∠B+∠E，
∵∠DFG是△AFC的外角，∴∠DFG=∠A+∠C，
∵∠DFG+∠DGF+∠D=
∴∠A+∠B+∠C+∠D+∠E=
故答案是：180. 如图,图案⑥是由图①~⑤中五种基本图形中的两种拼接而成的,则这两种基本图形是( )
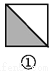
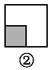
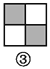
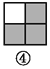
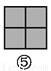
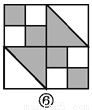
A. ①② B. ①③ C. ①④ D. ③⑤
B
【解析】根据已知图形，利用分割与组合的原理对图形进行分析即可．
【解析】
如图所示：图案⑥是由图①和图③这两种基本图形拼接而成的.
故选：B. 在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，下列等式中不一定成立的是（ ）
A. b=atanB B. a=ccosB C. c＝
D. a=bcosA
D
【解析】∵∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，
∴A.tanB= ，则b=atanB，故本选项正确，
B.cosB= ，故本选项正确，
C.sinA= ，故本选项正确，
D.cosA= ，故本选项错误，
故选D． 在Rt△ABC中，∠C=90°，如果AC：BC=3：4，求cosA的值.
【解析】分析:根据题意设AC=3x，BC=4x，故AB=5x，进而利用锐角三角函数关系求出答案．
本题解析：
∵在Rt△ABC中，∠C=90°，AC：BC=3：4，
∴设AC=3x，BC=4x，故AB=5x，
则cosA=
故答案为： 当角度在0°到90°之间变化时，函数值随着角度的增大而增大的三角函数是（ ）
A. 正弦和余弦 B. 正弦和正切 C. 余弦和正切 D. 正弦、余弦和正切
B
【解析】当角度在0°到90°之间变化时，函数值随着角度的增大而增大的三角函数是正弦和正切．
故选B． 在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，下列等式中不一定成立的是（ ）
A. b=atanB B. a=ccosB C. c＝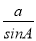
D. a=bcosA
D
【解析】∵∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，
∴A.tanB= ，则b=atanB，故本选项正确，
B.cosB= ，故本选项正确，
C.sinA= ，故本选项正确，
D.cosA= ，故本选项错误，
故选D． 小红到文具商店买彩笔，每打彩笔12支，售价18元，那么买彩笔所需的钱数y(元)与购买彩笔的支数x(支)之间的关系式为( )
A. y＝1.5x B. y＝x C. y＝12x D. y＝18x
A
【解析】根据钱数=单价×数量可得： .
故选A. 如图所示为农村居民住宅侧面截面图，屋坡AF、AG分别架在墙体的点B，点C处，且AB＝AC，侧面四边形BDEC为长方形．若测得∠FAG＝110°，则∠FBD＝( )
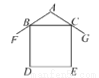
A. 35° B. 40° C. 55° D. 70°
C
【解析】在△ABC中，AB＝AC，∠BAC＝110°，根据等腰三角形的性质和三角形的内角和定理可得∠ABC=35°，由四边形BDEC为长方形可得∠DBC=90°，再由平角的定义可得∠FBD=180°-∠ABC-∠DBC=180°-35°-90°=55°，故选C.