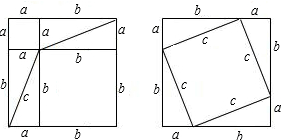
题目内容
6.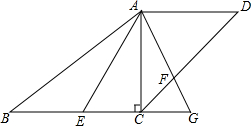 如图,梯形ABCD中,AD∥BC,对角线AC⊥BC,AD=9,AC=12,BC=16,点E是边BC上以点,且∠EAF=∠BAC,AF交CD于点F,交BC延长线于点G,求证:$\frac{BE}{FC}=\frac{5}{3}$.
如图,梯形ABCD中,AD∥BC,对角线AC⊥BC,AD=9,AC=12,BC=16,点E是边BC上以点,且∠EAF=∠BAC,AF交CD于点F,交BC延长线于点G,求证:$\frac{BE}{FC}=\frac{5}{3}$.
分析 通过△ABC∽△DCA,则有∠B=∠ACD,由∠EAF=∠BAC可得∠BAE=∠CAF,从而得到△ABE∽△ACF,然后根据相似三角形的性质即可解决问题.
解答 解:∵AC⊥BC,∴∠ACB=90°.
∵AD∥BC,∴∠DAC=∠ACB=90°.
∵AD=9,AC=12,BC=16,
∴AB=20,DC=15.
∵$\frac{BC}{AC}$=$\frac{AC}{AD}$=$\frac{4}{3}$,∠DAC=∠ACB,
∴△ABC∽△DCA,
∴∠B=∠ACD.
∵∠EAF=∠BAC,
∴∠BAE=∠CAF,
∴△ABE∽△ACF,
∴$\frac{AB}{AC}$=$\frac{BE}{CF}$=$\frac{20}{12}$=$\frac{5}{3}$.
点评 本题主要考查了相似三角形的判定与性质、等腰三角形的性质、勾股定理等知识,证到△ABE∽△ACF是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.如果甲数除以乙数的商为负数,那么下列说法正确且全面的是( )
| A. | 这两个数的绝对值相等而符号相反 | B. | 甲数为正,乙数为负 | ||
| C. | 甲数为正,乙数不等于0 | D. | 甲、乙两数异号 |
 如图,△DEF是△ABC经过位似变换得到的,位似中心是点O,确定点O的位置,如果OC=3.6cm,OF=2.4cm,求它们的相似比.
如图,△DEF是△ABC经过位似变换得到的,位似中心是点O,确定点O的位置,如果OC=3.6cm,OF=2.4cm,求它们的相似比.
 如图,⊙O的半径OD平分弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=6,CE=5,求CD的长.
如图,⊙O的半径OD平分弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=6,CE=5,求CD的长.