题目内容
18．左图的正方形是由1个边长为a的正方形和1个边长为b的正方形以及4个直角边分别为a、b斜边为c的直角三角形拼成的；右图的正方形是由1个边长为c的正方形和4个直角边分别为a、b，斜边为c的直角三角形拼成的．请用这两个图证明勾股定理．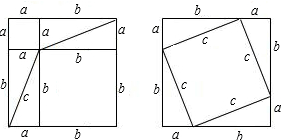
分析 通过两个组合正方形的面积之间相等的关系即可证明勾股定理．
解答 解：由图可知大正方形的边长为：a+b，则面积为（a+b）2，
图中把大正方形的面积分为了四部分，分别是：边长为a的正方形，边长为b的正方形，还有两个长为b，宽为a的长方形，
根据面积相等得：（a+b）2=a2+b2+4×$\frac{1}{2}$ab，
由右图可得（a+b）2=c2+4×$\frac{1}{2}$ab．
所以a2+b2=c2．
点评 本题考查利用图形面积的关系证明勾股定理，解题关键是利用三角形和正方形边长的关系进行组合图形．
练习册系列答案
相关题目
8．下列运算正确的是（ ）
| A． | $\sqrt{x}$+$\sqrt{5}$x=$\sqrt{6}$x | B． | 3$\sqrt{2}$-2$\sqrt{2}$=1 | C． | 2+$\sqrt{5}$=2$\sqrt{5}$ | D． | 5$\sqrt{x}$-b$\sqrt{x}$=（5-b） $\sqrt{x}$ |
9．若x、y为非零线段的长，则下列说法错误的是（ ）
| A． | 若$\frac{x}{y}$=$\frac{3}{2}$，则$\frac{y}{x}$=$\frac{2}{3}$ | B． | 若$\frac{x}{7}$=$\frac{y}{3}$，则$\frac{x+y}{x-y}$=$\frac{5}{2}$ | ||
| C． | 若$\frac{y}{x}$=$\frac{3}{7}$，则$\frac{x+y}{y}$=$\frac{10}{3}$ | D． | 若2x-5y=0，则$\frac{x-2y}{y}$=$\frac{1}{3}$ |
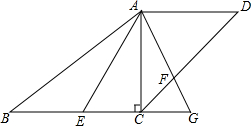如图，梯形ABCD中，AD∥BC，对角线AC⊥BC，AD=9，AC=12，BC=16，点E是边BC上以点，且∠EAF=∠BAC，AF交CD于点F，交BC延长线于点G，求证：$\frac{BE}{FC}=\frac{5}{3}$．
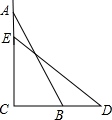如图，一架梯子AB长2.5m，顶端A靠在墙AC上，这时梯子下端B与墙角C距离1.5m，梯子滑动后停在DE的位置上，如果梯子底端向右滑动的距离与顶端向下滑动的距离相等，求梯子顶端A下滑了多少米．
7．己知二次函数y=-x2+bx+c中，函数值y与自变量x的部分对应值如下表：
（1）该二次函数的解析式为y=-x2+6x-8；
（2）请在表格内的空格中填入适当的数；
（3）直接写出y＞0时，x的取值范围2＜x＜4；
（4）请说明经过怎样平移函数y=-x2+bx+c的图象得到函数y=-x2的图象？
| x | … | 1 | 2 | 3 | 4 | 5 | … |
| -x2+bx+c | … | -3 | 1 | -3 | … |
（2）请在表格内的空格中填入适当的数；
（3）直接写出y＞0时，x的取值范围2＜x＜4；
（4）请说明经过怎样平移函数y=-x2+bx+c的图象得到函数y=-x2的图象？