题目内容
1.在直角坐标系中△ABC三个顶点坐标分别为A(7,1)、B(8,2)、C(9,0).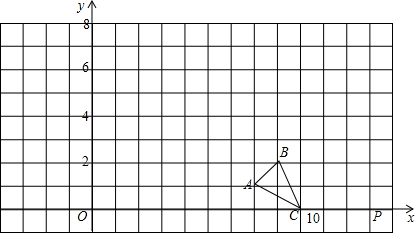
(1)请在图中画出△ABC的一个以点P (12,0)为位似中心,相似比为3的位似图形△A′B′C′(要求与△ABC同在P点一侧);
(2)请直接写出点B′及点C′的坐标;
(3)求线段BC的对应线段B′C′所在直线的解析式.
分析 (1)根据画位似图形的一般步骤和相似比找出图形;
(2)根据相似比和相似三角形的性质求出点B′及点C′的坐标;
(3)运用待定系数法求出一次函数解析式.
解答  解:(1)如图△A′B′C′即为所求;
解:(1)如图△A′B′C′即为所求;
(2)∵△ABC与△A′B′C′的相似比为1:3,
∴B′(0,6),C′(3,0);
(3)设B′C′所在直线的解析式为y=kx+b,
$\left\{\begin{array}{l}{b=6}\\{3k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-2}\\{b=6}\end{array}\right.$,
∴B′C′所在直线的解析式y=-2x+6.
点评 本题考查的是作图-位似变换、待定系数法求一次函数解析式,掌握画位似图形的一般步骤为:①确定位似中心,②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,得到放大或缩小的图形是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
12. 如图,把长方形ABCD沿EF对折后,使四边形ABFE与四边形HGFE重合,若∠1=50°,则∠AEF的度数为( )
如图,把长方形ABCD沿EF对折后,使四边形ABFE与四边形HGFE重合,若∠1=50°,则∠AEF的度数为( )
 如图,把长方形ABCD沿EF对折后,使四边形ABFE与四边形HGFE重合,若∠1=50°,则∠AEF的度数为( )
如图,把长方形ABCD沿EF对折后,使四边形ABFE与四边形HGFE重合,若∠1=50°,则∠AEF的度数为( )| A. | 110° | B. | 115° | C. | 120° | D. | 130° |
9.若x、y为非零线段的长,则下列说法错误的是( )
| A. | 若$\frac{x}{y}$=$\frac{3}{2}$,则$\frac{y}{x}$=$\frac{2}{3}$ | B. | 若$\frac{x}{7}$=$\frac{y}{3}$,则$\frac{x+y}{x-y}$=$\frac{5}{2}$ | ||
| C. | 若$\frac{y}{x}$=$\frac{3}{7}$,则$\frac{x+y}{y}$=$\frac{10}{3}$ | D. | 若2x-5y=0,则$\frac{x-2y}{y}$=$\frac{1}{3}$ |
16.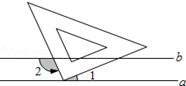 如图,小华把三角板的直角顶点放在直线a上,两条直角边与直线b相交,如果a∥b,且∠1=40°,则∠2的度数为( )
如图,小华把三角板的直角顶点放在直线a上,两条直角边与直线b相交,如果a∥b,且∠1=40°,则∠2的度数为( )
 如图,小华把三角板的直角顶点放在直线a上,两条直角边与直线b相交,如果a∥b,且∠1=40°,则∠2的度数为( )
如图,小华把三角板的直角顶点放在直线a上,两条直角边与直线b相交,如果a∥b,且∠1=40°,则∠2的度数为( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
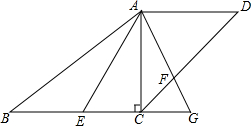 如图,梯形ABCD中,AD∥BC,对角线AC⊥BC,AD=9,AC=12,BC=16,点E是边BC上以点,且∠EAF=∠BAC,AF交CD于点F,交BC延长线于点G,求证:$\frac{BE}{FC}=\frac{5}{3}$.
如图,梯形ABCD中,AD∥BC,对角线AC⊥BC,AD=9,AC=12,BC=16,点E是边BC上以点,且∠EAF=∠BAC,AF交CD于点F,交BC延长线于点G,求证:$\frac{BE}{FC}=\frac{5}{3}$.