题目内容
16. 如图,△DEF是△ABC经过位似变换得到的,位似中心是点O,确定点O的位置,如果OC=3.6cm,OF=2.4cm,求它们的相似比.
如图,△DEF是△ABC经过位似变换得到的,位似中心是点O,确定点O的位置,如果OC=3.6cm,OF=2.4cm,求它们的相似比.
分析 由△DEF是△ABC经过位似变换得到的,根据位似图形的对应顶点的连线过位似中心,即可确定点O的位置;然后由OC=3.6cm,OF=2.4cm,即可求得它们的相似比.
解答  解:如图,连接CF,BE,则CF与BE的交点即为位似中心是点O.
解:如图,连接CF,BE,则CF与BE的交点即为位似中心是点O.
∵OC=3.6cm,OF=2.4cm,
∴它们的相似比为:3.6:2.4=3:2.
点评 此题考查了位似变换.注意位似图形的对应顶点的连线过位似中心.

练习册系列答案
相关题目
1.能判定△ABC∽△A′B′C′的条件是( )
| A. | $\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$,∠B=∠B′ | B. | $\frac{AB}{A′C′}$=$\frac{A′B′}{AC}$,∠B=∠B′ | ||
| C. | $\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$,∠A=∠A′ | D. | $\frac{AB}{A′B′}$=$\frac{AC}{B′C′}$,∠A=∠A′ |
8.下列运算正确的是( )
| A. | $\sqrt{x}$+$\sqrt{5}$x=$\sqrt{6}$x | B. | 3$\sqrt{2}$-2$\sqrt{2}$=1 | C. | 2+$\sqrt{5}$=2$\sqrt{5}$ | D. | 5$\sqrt{x}$-b$\sqrt{x}$=(5-b) $\sqrt{x}$ |
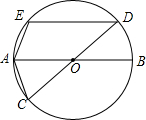 如图,AB,CD是⊙O的直径,弦DE∥AB,则AC与AE的大小关系是AC=AE.
如图,AB,CD是⊙O的直径,弦DE∥AB,则AC与AE的大小关系是AC=AE. 如图,已知点M是反比例函数y=-$\frac{6}{x}$的图象上任意一点,过点M分别作x轴、y轴的垂线,垂足依次为P,Q,那么四边形OQMP的面积为6.
如图,已知点M是反比例函数y=-$\frac{6}{x}$的图象上任意一点,过点M分别作x轴、y轴的垂线,垂足依次为P,Q,那么四边形OQMP的面积为6.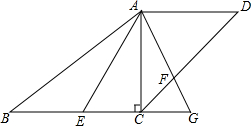 如图,梯形ABCD中,AD∥BC,对角线AC⊥BC,AD=9,AC=12,BC=16,点E是边BC上以点,且∠EAF=∠BAC,AF交CD于点F,交BC延长线于点G,求证:$\frac{BE}{FC}=\frac{5}{3}$.
如图,梯形ABCD中,AD∥BC,对角线AC⊥BC,AD=9,AC=12,BC=16,点E是边BC上以点,且∠EAF=∠BAC,AF交CD于点F,交BC延长线于点G,求证:$\frac{BE}{FC}=\frac{5}{3}$.