题目内容
11. 如图,⊙O的半径OD平分弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=6,CE=5,求CD的长.
如图,⊙O的半径OD平分弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=6,CE=5,求CD的长.
分析 由OD⊥AB,根据垂径定理得到AC=BC=$\frac{1}{2}$AB=4,由AE是直径,根据圆周角定理得到∠ABE=90°,根据勾股定理求得AE,BE,再利用OC是△ABE的中位线得到OC=$\frac{1}{2}$CE=2,然后根据CD=OD-OC可计算出结果.
解答 解:连结BE,如图,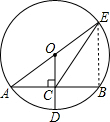
∵OD⊥AB,
∴AC=BC=$\frac{1}{2}$AB=$\frac{1}{2}$×6=3,
∵CE=5,BC=4,
∵AE是直径,
∴∠ABE=90°,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{{6}^{2}+{5}^{2}}$=$\sqrt{61}$,
在Rt△BCE中,∵BE2=CE2-BC2,
即BE2=52-32=16,
∴BE=4,
∵OC是△ABE的中位线,
∴OC=$\frac{1}{2}$BE=2,
∴CD=$\frac{\sqrt{61}}{2}$-2=$\frac{\sqrt{61}-4}{2}$.
点评 本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理、圆周角定理.

练习册系列答案
相关题目
1.能判定△ABC∽△A′B′C′的条件是( )
| A. | $\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$,∠B=∠B′ | B. | $\frac{AB}{A′C′}$=$\frac{A′B′}{AC}$,∠B=∠B′ | ||
| C. | $\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$,∠A=∠A′ | D. | $\frac{AB}{A′B′}$=$\frac{AC}{B′C′}$,∠A=∠A′ |
19.如图,下列四个几何体中,俯视图不同与其他几何体的是( )


| A. | ④ | B. | ③ | C. | ② | D. | ① |
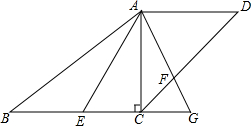 如图,梯形ABCD中,AD∥BC,对角线AC⊥BC,AD=9,AC=12,BC=16,点E是边BC上以点,且∠EAF=∠BAC,AF交CD于点F,交BC延长线于点G,求证:$\frac{BE}{FC}=\frac{5}{3}$.
如图,梯形ABCD中,AD∥BC,对角线AC⊥BC,AD=9,AC=12,BC=16,点E是边BC上以点,且∠EAF=∠BAC,AF交CD于点F,交BC延长线于点G,求证:$\frac{BE}{FC}=\frac{5}{3}$. 建立直角坐标系,描出下列各点A(-2,2),B(-1,0),C(0,2)
建立直角坐标系,描出下列各点A(-2,2),B(-1,0),C(0,2)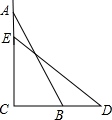 如图,一架梯子AB长2.5m,顶端A靠在墙AC上,这时梯子下端B与墙角C距离1.5m,梯子滑动后停在DE的位置上,如果梯子底端向右滑动的距离与顶端向下滑动的距离相等,求梯子顶端A下滑了多少米.
如图,一架梯子AB长2.5m,顶端A靠在墙AC上,这时梯子下端B与墙角C距离1.5m,梯子滑动后停在DE的位置上,如果梯子底端向右滑动的距离与顶端向下滑动的距离相等,求梯子顶端A下滑了多少米.