��Ŀ����
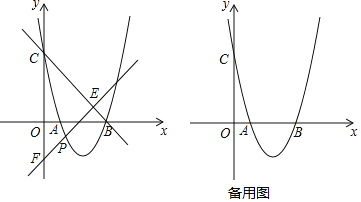
��ͼ��������y=x2+bx+c��x�ύ��A��B���㣬B������Ϊ��4��0������y�ύ�ڵ�C��0��4����
��1���������ߵĽ���ʽ��
��2����P��x���·����������ϣ�����P��ֱ��y=x+m��ֱ��BC���ڵ�E����y�ύ�ڵ�F����PE+EF�����ֵ��
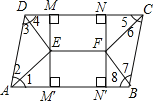
��3����DΪ�����߶Գ�����һ�㣮
�ٵ���BCD����BCΪֱ�DZߵ�ֱ��������ʱ��ֱ��д����D�����ꣻ
������BCD����������Σ�ֱ��д����D��������n��ȡֵ��Χ��
��ϰ��ϵ�д�
 ��ѧ��������������Ͼ���ѧ������ϵ�д�
��ѧ��������������Ͼ���ѧ������ϵ�д� �ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�
�ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�
�����Ŀ
���꼶һ�չ�ˡ���һ�����顱�Ļ����ί���ѧ���Ķ��鼮������������ʾ����飬�ʾ������ˡ�С˵����Ϸ�硱��ɢ�ġ����������ĸ�ѡ�ÿλͬѧ��ѡһ����ݵ��������������²�������Ƶ���ֲ���������ͳ��ͼ��
����� | ��Ƶ���������� | ��Ƶ�� |
��С˵ | 16 | �� |
��Ϸ�� | 4 | |
��ɢ�� | a | �� |
������ | b | |
���ϼ� | ��1 |
����ͼ���ṩ����Ϣ������������⣺
��1��ֱ��д��a��b��m��ֵ��
��2���ڵ����ʾ��У��ס��ҡ���������λͬѧѡ���ˡ�Ϸ�硱�࣬�ִ�������λͬѧ������ѡ��2��ͬѧ�μ�ѧУ��Ϸ����ȤС�飬�����б�������״ͼ�ķ�������ѡȡ��2��ǡ���Һͱ��ĸ��ʣ�



 ��
�� ��a2��b2��
��a2��b2��







 =
= +
+ ����ʵ��A=_____��
����ʵ��A=_____��