题目内容
已知⊙O的半径3cm,其中一弧长2πcm,求这弧所对的弦长.
考点:弧长的计算,垂径定理
专题:
分析:先利用弧长计算公式求出AB弧所对圆心角∠AOB=120°,再作弦心距OC,根据等腰三角形三线合一的性质得出∠AOC=
∠AOB=60°,由正弦函数定义求出AC,再根据垂径定理得出AB=2AC.
| 1 |
| 2 |
解答: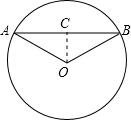 解:如图,已知⊙O的半径3cm,弧AB长2πcm,设∠AOB=n°,
解:如图,已知⊙O的半径3cm,弧AB长2πcm,设∠AOB=n°,
则
=2π,解得n=120°.
作OC⊥AB于C,则AB=2AC.
∵OA=OB,
∴∠AOC=
∠AOB=60°,
∴AC=OA•sin∠AOC=3×
=
,
∴AB=2AC=3
(cm).
 解:如图,已知⊙O的半径3cm,弧AB长2πcm,设∠AOB=n°,
解:如图,已知⊙O的半径3cm,弧AB长2πcm,设∠AOB=n°,则
| nπ×3 |
| 180 |
作OC⊥AB于C,则AB=2AC.
∵OA=OB,
∴∠AOC=
| 1 |
| 2 |
∴AC=OA•sin∠AOC=3×
| ||
| 2 |
3
| ||
| 2 |
∴AB=2AC=3
| 3 |
点评:本题考查了弧长的计算,等腰三角形的性质,正弦函数的定义,垂径定理,难度适中.求出∠AOB=120°是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
两个数的和为零,则这两个数( )
| A、一个为正数,一个为负数 |
| B、互为相反数 |
| C、一个为零,一个为负数 |
| D、至少有一个为负数 |

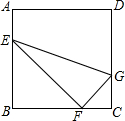 如图,边长为6cm的正方形ABCD中,点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向移动,点E、G的速度均为1cm/s,点F的速度为2cm/s.当点F追上点G(即点F与点G重合)时,三个点都停止运动,设运动时间为t(t>0).
如图,边长为6cm的正方形ABCD中,点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向移动,点E、G的速度均为1cm/s,点F的速度为2cm/s.当点F追上点G(即点F与点G重合)时,三个点都停止运动,设运动时间为t(t>0).
 如图,在?ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,求点E到直线AB的距离.
如图,在?ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,求点E到直线AB的距离.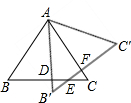 将两块形状完全相同的等腰直角三角板摆放成如图所示的样子,假设图形中所有点、线都在同一平面内,那么图中共有多少对全等三角形?把它们一一写出,找出一对说出理由. (提示:等腰直角三角板两直角边相等,两锐角都是45°)
将两块形状完全相同的等腰直角三角板摆放成如图所示的样子,假设图形中所有点、线都在同一平面内,那么图中共有多少对全等三角形?把它们一一写出,找出一对说出理由. (提示:等腰直角三角板两直角边相等,两锐角都是45°)