题目内容
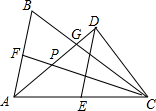 如图,在△ABC中,过C作∠BAC的平分线AD的垂线,垂足为D,AD交BC于G,DE∥AB交AC于E.
如图,在△ABC中,过C作∠BAC的平分线AD的垂线,垂足为D,AD交BC于G,DE∥AB交AC于E.(1)求证:AE=CE;
(2)作∠BCA的平分线CF交AD于P,交AB于F,求证:∠PCD=
| 1 |
| 2 |
(3)在(2)的条件下,若∠B=60°,求证:AF+GC=AC.
考点:全等三角形的判定与性质,线段垂直平分线的性质,等腰三角形的性质,相似三角形的判定与性质
专题:计算题
分析:(1)延长CD,交AB的延长线于H,由AD垂直于CH,AD为角平分线,得到三角形ACH为等腰三角形,利用三线合一得到D为CH中点,即CD=DH,由DE与AH平行,利用平行线等分线段定理即可得证;
(2)连接HP,HG,由AD垂直平分CH,得到HG=CG,HP=CP,AH=AC,利用等边对等角得到三对角相等,进而得到∠AHP=∠ACP,再由∠CFH为公共角,利用两对对应角相等的两三角形相似得到三角形HFP与三角形CFB相似,由相似三角形对应角相等得到∠FPH=∠CBF,由CP=HP,利用等边对等角且外角性质,等量代换即可得证;
(3)由(2)得到∠PCD与∠PHD的度数,求出∠CPD与∠HPD的度数,根据CF为角平分线得到HP为∠FHP的平分线,得到一对角相等,利用ASA得到三角形HFP与三角形HGP全等,由全等三角形对应边相等得到HF=GH=CG,由AF+CG等量代换即可得证.
(2)连接HP,HG,由AD垂直平分CH,得到HG=CG,HP=CP,AH=AC,利用等边对等角得到三对角相等,进而得到∠AHP=∠ACP,再由∠CFH为公共角,利用两对对应角相等的两三角形相似得到三角形HFP与三角形CFB相似,由相似三角形对应角相等得到∠FPH=∠CBF,由CP=HP,利用等边对等角且外角性质,等量代换即可得证;
(3)由(2)得到∠PCD与∠PHD的度数,求出∠CPD与∠HPD的度数,根据CF为角平分线得到HP为∠FHP的平分线,得到一对角相等,利用ASA得到三角形HFP与三角形HGP全等,由全等三角形对应边相等得到HF=GH=CG,由AF+CG等量代换即可得证.
解答: 证明:(1)延长CD,交AB的延长线于H,
证明:(1)延长CD,交AB的延长线于H,
∵AD⊥CH,即∠ADC=∠ADH=90°,∠HAD=∠CAD,
∴∠H=∠ACH,
∴AH=AC,即△ACH为等腰三角形,
∴CD=DH,
∵DE∥AH,
∴AE=CE;
(2)连接HP,HG,
∵AD为HC的垂直平分线,
∴∠AHP=∠ACP,
∵∠CFH为公共角,
∴△HFP∽△CFB,
∴∠FPH=∠CBF,
∵CP=HP,
∴∠FPH=∠PCD+∠PHD=2∠PCD,
∴∠PCD=
∠CBF;
(3)由(2)得:∠PCD=30°=∠PHD,
∴∠CPD=∠HPD=60°,
∵CF为∠ACB的平分线,
∴HP为∠FHG的平分线,
在△HFP和△HGP中,
,
∴△HFP≌和△HGP(ASA),
∴HG=HF=CG,
则CG+AF=HF+AF=AH=AC.
 证明:(1)延长CD,交AB的延长线于H,
证明:(1)延长CD,交AB的延长线于H,∵AD⊥CH,即∠ADC=∠ADH=90°,∠HAD=∠CAD,
∴∠H=∠ACH,
∴AH=AC,即△ACH为等腰三角形,
∴CD=DH,
∵DE∥AH,
∴AE=CE;
(2)连接HP,HG,
∵AD为HC的垂直平分线,
∴∠AHP=∠ACP,
∵∠CFH为公共角,
∴△HFP∽△CFB,
∴∠FPH=∠CBF,
∵CP=HP,
∴∠FPH=∠PCD+∠PHD=2∠PCD,
∴∠PCD=
| 1 |
| 2 |
(3)由(2)得:∠PCD=30°=∠PHD,
∴∠CPD=∠HPD=60°,
∵CF为∠ACB的平分线,
∴HP为∠FHG的平分线,
在△HFP和△HGP中,
|
∴△HFP≌和△HGP(ASA),
∴HG=HF=CG,
则CG+AF=HF+AF=AH=AC.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
下列平面图形经过折叠后,不能围成正方体的是( )
A、 |
B、 |
C、 |
D、 |

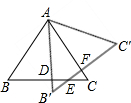 将两块形状完全相同的等腰直角三角板摆放成如图所示的样子,假设图形中所有点、线都在同一平面内,那么图中共有多少对全等三角形?把它们一一写出,找出一对说出理由. (提示:等腰直角三角板两直角边相等,两锐角都是45°)
将两块形状完全相同的等腰直角三角板摆放成如图所示的样子,假设图形中所有点、线都在同一平面内,那么图中共有多少对全等三角形?把它们一一写出,找出一对说出理由. (提示:等腰直角三角板两直角边相等,两锐角都是45°) 如图,已知线段a,点A、B在直线l的同侧,在直线l上,求作点P、Q(点P在点Q的左侧)且PQ=a,使四边形APQB的周长最小.
如图,已知线段a,点A、B在直线l的同侧,在直线l上,求作点P、Q(点P在点Q的左侧)且PQ=a,使四边形APQB的周长最小.