题目内容
12.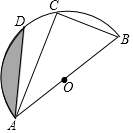 已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为12,且BC=6,∠DAB=45°.(1)求∠DAC的度数;(2)求图中阴影部分的面积(结果保留π).
已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为12,且BC=6,∠DAB=45°.(1)求∠DAC的度数;(2)求图中阴影部分的面积(结果保留π).
分析 (1)根据含30°角的直角三角形性质求出∠CAB,即可得出答案;
(2)连接OD,求出∠DOA,分别求出扇形AOD和△AOD面积,即可得出答案.
解答 解:(1)∵AB是直径,
∴∠ACB=90°,
又∵BC=6,AB=12,
∴BC=$\frac{1}{2}$AB,
∴∠BAC=30°,
∴∠DAC=∠DAB-∠BAC=45°-30°=15°;
(2)连接OD,
∵直径AB=12,
∴半径OD=OA=6,
∵OA=OD,∠DAB=45°,
∴∠ADO=∠DAB=45°,
∴∠AOD=90°,
∴阴影部分的面积S=S扇形AOD-S△AOD=$\frac{90•π×{6}^{2}}{360}$-$\frac{1}{2}×6×6$=9π-18.
点评 本题考查了含30°角的直角三角形性质,扇形的面积计算,圆周角定理等知识点,能求出∠CAB=30°和∠AOD=90°是解此题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
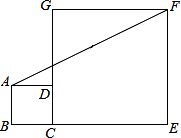 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,C到直线AF的距离是$\frac{3\sqrt{5}}{5}$.
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,C到直线AF的距离是$\frac{3\sqrt{5}}{5}$.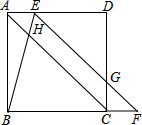 如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H,AE=CF,BE=EG.
如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H,AE=CF,BE=EG.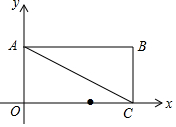 如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=1,OC=2,点D在边OC上且OD=1.25.
如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=1,OC=2,点D在边OC上且OD=1.25.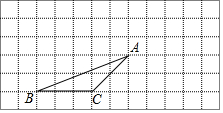 画图并填空:如图,△ABC的顶点都在每个边长为1个单位长度的方格纸的格点上,将△ABC向右平移3格,再向上平移2格.
画图并填空:如图,△ABC的顶点都在每个边长为1个单位长度的方格纸的格点上,将△ABC向右平移3格,再向上平移2格.