题目内容
17．不等式|x-1|＜1的解集是（ ）| A． | x＞2 | B． | x＜0 | C． | 1＜x＜2 | D． | 0＜x＜2 |
分析 根据绝对值性质分x-1＞0、x-1＜0，去绝对值符号后解相应不等式可得x的范围．
解答 解：①当x-1≥0，即x≥1时，原式可化为：x-1＜1，
解得：x＜2，
∴1≤x＜2；
②当x-1＜0，即x＜1时，原式可化为：1-x＜1，
解得：x＞0，
∴0＜x＜1，
综上，该不等式的解集是0＜x＜2，
故选：D．
点评 本题主要考查解一元一次不等式的能力，根据绝对值性质分类讨论是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
12．
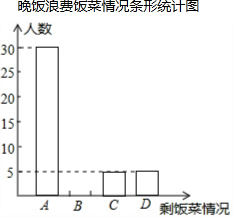自从2012年12月4日中央公布“八项规定”以来，某中学积极开展“厉行勤俭节约，反对铺张浪费”的活动．为此，校学生会在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查，调查内容分为四种：A．饭和菜全部吃完；B．有剩饭但菜吃完；C．饭吃完但菜有剩；D．饭和菜都有剩．根据统计结果绘制了如下不完整的统计图表，根据所提供的信息回答下列问题：
晚饭浪费饭菜情况统计表
（1）晚饭浪费饭菜情况统计表中的n=10，m=60%．
（2）请把“晚饭浪费饭菜条形统计图”补充完整；
（3）若绘制““晚饭浪费饭菜条形统计图””，调查内容为“饭吃完但菜有剩”所对应的圆心角等于36度
（4）该中学有学生2200名，请估计这餐晚饭中“有饭吃但菜吃完”和“饭吃完但菜有剩”的学生有660人．
自从2012年12月4日中央公布“八项规定”以来，某中学积极开展“厉行勤俭节约，反对铺张浪费”的活动．为此，校学生会在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查，调查内容分为四种：A．饭和菜全部吃完；B．有剩饭但菜吃完；C．饭吃完但菜有剩；D．饭和菜都有剩．根据统计结果绘制了如下不完整的统计图表，根据所提供的信息回答下列问题：晚饭浪费饭菜情况统计表
| 选项 | 频数 | 频率 |
| A | 30 | m |
| B | n | 20% |
| C | 5 | 10% |
| D | 5 | 10% |
（2）请把“晚饭浪费饭菜条形统计图”补充完整；
（3）若绘制““晚饭浪费饭菜条形统计图””，调查内容为“饭吃完但菜有剩”所对应的圆心角等于36度
（4）该中学有学生2200名，请估计这餐晚饭中“有饭吃但菜吃完”和“饭吃完但菜有剩”的学生有660人．