题目内容
9.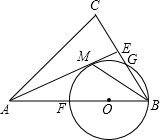 已知如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于M,经过B、M两点的⊙O交BC于点G,交AB于点F,BF恰为⊙O的直径.
已知如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于M,经过B、M两点的⊙O交BC于点G,交AB于点F,BF恰为⊙O的直径.①不作辅助线,写出图中相等的线段和能知道度数的角.
②求证:AE与⊙O相切.
分析 (1)根据等腰三角形三线合一的性质即可得出CE=BE,∠AEC=∠AEB=90°,
(2)连接OM,可得∠OMB=∠OBM=∠MBE,根据∠OMB+∠BME=∠MBE+∠BME=90°即可证明;
解答 (1)解:∵AB=AC,AE是角平分线,
∴CE=BE,∠AEC=∠AEB=90°;
(2)证明:连接OM,
∵OM=OB,
∴∠OMB=∠OBM,
∵∠OBM=∠MBE,
∴∠OMB=∠OBM=∠MBE
又∵AB=AC,AE是角平分线,
∴AE⊥BC,
∴∠OMB+∠BME=∠MBE+∠BME=90°,
∴∠AMO=90°,
∴AE与⊙O相切.
点评 本题考查了等腰三角形三线合一的性质以及切线的判定,作出辅助线构建等腰三角形是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
20.直线y=5x+5和y=3x-1的交点必在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.已知直角三角形的三边长为三个连续整数,那么,这个三角形的面积是( )
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
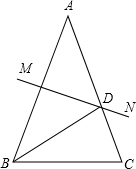 如图,三角形ABC中,AB=AC,∠A=40度,AB的垂直平分线MN交AC于D,连接BD,∠DBC等于30度.
如图,三角形ABC中,AB=AC,∠A=40度,AB的垂直平分线MN交AC于D,连接BD,∠DBC等于30度. 如图,在△ABC中,AB=2015,AC=2013,AD为中线,则△ABD与△ACD的周长之差=2.
如图,在△ABC中,AB=2015,AC=2013,AD为中线,则△ABD与△ACD的周长之差=2.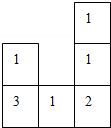 如图,是一个由若干同样大小的正方体搭成的几何体俯视图,小正方形中的数字表示在该位置的立方体的个数.
如图,是一个由若干同样大小的正方体搭成的几何体俯视图,小正方形中的数字表示在该位置的立方体的个数.