题目内容
1．已知直角三角形的三边长为三个连续整数，那么，这个三角形的面积是（ ）| A． | 6 | B． | 8 | C． | 10 | D． | 12 |
分析 设这三边长分别为x，x+1，x+2，根据勾股定理可得出（x+2）2=（x+1）2+x2，解方程可求得三角形的三边长，利用直角三角形的性质直接求得面积即可．
解答 解：设这三边长分别为x，x+1，x+2，
根据勾股定理得：（x+2）2=（x+1）2+x2
解得：x=-1（不合题意舍去），或x=3，
∴x+1=4，x+2=5，
则三边长是3，4，5，
∴三角形的面积=$\frac{1}{2}$××4=6；
故选：A．
点评 本题考查了勾股定理、直角三角形面积的计算方法；熟练掌握勾股定理，由勾股定理得出方程是解决问题的关键．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
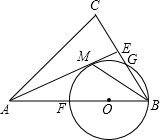已知如图，在△ABC中，AB=AC，AE是角平分线，BM平分∠ABC交AE于M，经过B、M两点的⊙O交BC于点G，交AB于点F，BF恰为⊙O的直径．
抛物线y=ax2+bx+c（a≠0）经过A（-1，0），B（0，-3），C（3，0）三点．