题目内容
3.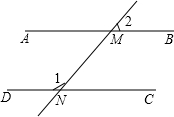 如图所示,已知∠1的度数是它的补角的3倍,∠2=45°,试说明AB∥CD.
如图所示,已知∠1的度数是它的补角的3倍,∠2=45°,试说明AB∥CD.
分析 首先根据两角互补的定义和已知列出方程,求出∠1的度数,然后由对顶角的性质可知∠AMN=∠2,从而发现∠1+∠AMN=180°,根据平行线的判定得出AB∥CD.
解答 解:AB∥CD.
理由如下:
∵∠1+∠MNC=180°,∠MNC=$\frac{1}{3}$∠1,
∴∠1=135°.
又∵∠AMN=∠2=45°,
∴∠1+∠AMN=180°.
∴AB∥CD.
点评 本题主要考查了两角互补的定义,对顶角的性质及平行线的判定.解题的关键是:根据两角互补的定义和已知列出方程,求出∠1的度数.

练习册系列答案
相关题目
13.下列各式不是一元一次不等式组的是( )
| A. | $\left\{\begin{array}{l}{x>3}\\{x<1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{3x<5}\\{2x-1<9}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-1>3}\\{y+2<0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-1>3}\\{x-3<2}\\{2x-1<5}\end{array}\right.$ |
9.已知不等式mx+n>0的解集为x<2,则不等式(3m-n)x<2m+6n的解集是( )
| A. | x<-2 | B. | x>-2 | C. | x<14 | D. | x>14 |
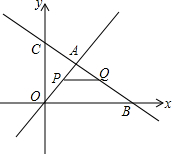 如图,在平面直角坐标系中,两个函数y=x,y=-$\frac{1}{2}$x+6的图象交于点A,动点P从点O开始沿OA方向以每秒$\sqrt{2}$个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设正方形边长为m.|
如图,在平面直角坐标系中,两个函数y=x,y=-$\frac{1}{2}$x+6的图象交于点A,动点P从点O开始沿OA方向以每秒$\sqrt{2}$个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设正方形边长为m.| 为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行),通道水平宽度BC为8米,∠BCD=135°,通道斜面CD的长为6米,通道斜面AB的坡度i=1:$\sqrt{2}$.
为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行),通道水平宽度BC为8米,∠BCD=135°,通道斜面CD的长为6米,通道斜面AB的坡度i=1:$\sqrt{2}$.
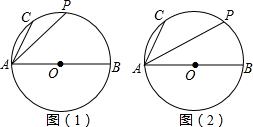
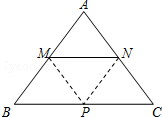 在等腰△ABC中,AB=AC=5,BC=6.动点M、N分别在两腰AB、AC上(M不与A、B重合,N不与A、C重合),且MN∥BC.将△AMN沿MN所在的直线折叠,使点A的对应点为P.
在等腰△ABC中,AB=AC=5,BC=6.动点M、N分别在两腰AB、AC上(M不与A、B重合,N不与A、C重合),且MN∥BC.将△AMN沿MN所在的直线折叠,使点A的对应点为P.