题目内容
15.如图,AB是⊙O的直径,C、P是弧AB上两点,AB=13,AC=5.(1)如图(1),若点P是弧AB的中点,求PA的长;
(2)如图(2),若点P是弧BC的中点,求PA的长;
(3)题干不变,问题(1)变为:若点P是弦AC的中点,求PA的长;
(4)题干不变,问题(2)变为:若点P是弧BAC的中点,求PA的长.
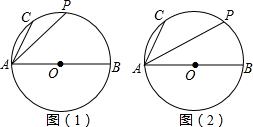
分析 (1)根据圆周角的定理,∠APB=90°,p是弧AB的中点,所以三角形APB是等腰三角形,利用特殊角的三角函数即可求得;
(2)根据垂径定理得出OP垂直平分BC,得出OP∥AC,从而得出△ACB∽△0NP,根据对应边成比例求得ON、AN的长,利用勾股定理求得NP的长,进而求得PA;
(3)利用勾股定理可得BC长,根据中位线性质,可得OP=$\frac{1}{2}BC$,利用勾股定理得AP;
(4)若点P是弧BAC的中点,∠AOP=∠BOP=90°,利用特殊角的三角函数易得AP=$\sqrt{2}$AO=$\frac{13\sqrt{2}}{2}$.
解答 解:(1)如图(1)所示,连接PB,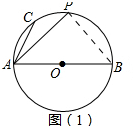
∵AB是⊙O的直径且P是$\widehat{AB}$的中点,
∴∠PAB=∠PBA=45°,∠APB=90°,
又∵在等腰三角形△APB中有AB=13,
∴PA=$\frac{AB}{\sqrt{2}}$=$\frac{13}{\sqrt{2}}$=$\frac{13\sqrt{2}}{2}$;
(2)如图(2)所示:连接BC.OP相交于M点,作PN⊥AB于点N,
∵P点为弧BC的中点,
∴OP⊥BC,∠OMB=90°,
又因为AB为直径,
∴∠ACB=90°,
∴∠ACB=∠OMB,
∴OP∥AC,
∴∠CAB=∠POB,
又因为∠ACB=∠ONP=90°,
∴△ACB∽△0NP
∴$\frac{AB}{OP}$=$\frac{AC}{ON}$,
又∵AB=13 AC=5 OP=$\frac{13}{2}$,
代入得 ON=$\frac{5}{2}$,
∴AN=OA+ON=9
∴在Rt△OPN中,有NP2=0P2-ON2=36
在Rt△ANP中 有PA=$\sqrt{{AN}^{2}{+NP}^{2}}$=$\sqrt{117}$=3$\sqrt{13}$
∴PA=3$\sqrt{13}$;
(3)如图3,取AC中点P,连接OP,
∵AB是⊙O的直径,AB=13,AC=5
∴BC=$\sqrt{{AB}^{2}{-AC}^{2}}$=12,
∴OP为△ABC的中位线,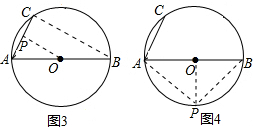
∴OP=$\frac{1}{2}BC$=6,
∴AP=$\sqrt{{OA}^{2}{-OE}^{2}}$=$\sqrt{{(\frac{13}{2})}^{2}{-6}^{2}}$=$\frac{5}{2}$;
(4)如图4,连接AP,BP,OP,
∵点P是弧BAC的中点,AB是⊙O的直径,
∴∠AOP=∠BOP=90°,
∴△AOP为等腰直角三角形,
∴AP=$\sqrt{2}$AO=$\frac{13\sqrt{2}}{2}$.
点评 本题考查了圆周角的定理,垂径定理,勾股定理,等腰三角形判定和性质,相似三角形的判定和性质,作出辅助线是本题的关键.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案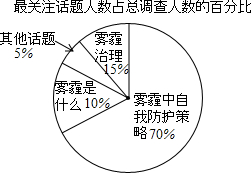 2015年3月3日到3月15日,两会在京矩形,雾霾防治问题受到国民的普遍关注,某报社决定以“对于雾霾,你最关注的话题是什么”为主题,通过街头随访和网络调查两种方式进行调查,根据调查所得数据绘制了表格.
2015年3月3日到3月15日,两会在京矩形,雾霾防治问题受到国民的普遍关注,某报社决定以“对于雾霾,你最关注的话题是什么”为主题,通过街头随访和网络调查两种方式进行调查,根据调查所得数据绘制了表格. | 最关注的话题 | 街头随访/人 | 网络调查/人 | 合计/人 |
| 雾霾是什么 | 80 | 120 | 200 |
| 雾霾治理 | 40%a | 60%a | a |
| 雾霾中自我防护策略 | 800 | 600 | 1400 |
| 其他话题 | 40 | 60 | 100 |
(2)请你将以上表格中空白处补充完整;
(3)若在接受街头随访的人员中随机抽出一人,则抽到最关注“雾霾中自我防护策略”人员的概率是$\frac{10}{13}$;
(4)通过这次调查,你有什么想法?
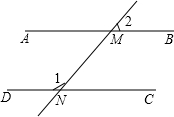 如图所示,已知∠1的度数是它的补角的3倍,∠2=45°,试说明AB∥CD.
如图所示,已知∠1的度数是它的补角的3倍,∠2=45°,试说明AB∥CD.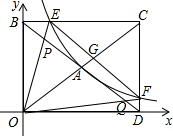 如图,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过矩形OBCD对角线的交点A,分别与CD、BC交于点F、点E,若三角形ODF的面积为2.
如图,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过矩形OBCD对角线的交点A,分别与CD、BC交于点F、点E,若三角形ODF的面积为2.
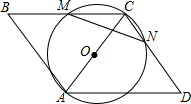 如图,在平行四边形ABCD中,以对角线AC为直径的⊙O分别交BC,CD于M,N.若AB=13,BC=14,CM=9,则MN的长度为$\frac{180}{13}$.
如图,在平行四边形ABCD中,以对角线AC为直径的⊙O分别交BC,CD于M,N.若AB=13,BC=14,CM=9,则MN的长度为$\frac{180}{13}$.