题目内容
⊙I切△ABC于D、E、F,∠C=60°,∠EIF=100°,则∠B= .
考点:三角形的内切圆与内心
专题:
分析:根据题意画出符合题意得两种情况:①当E在AC上,F在AB上,D在BC上时,根据切线性质求出∠CEI=∠CDI=∠BDI=∠BFI=90°,即可求出答案;②当E在AB上,F在BC上,D在AC上时,根据切线性质求出∠BEI=∠BFI=90°,即可求出答案.
解答:解:①当E在AC上,F在AB上,D在BC上时,如图1,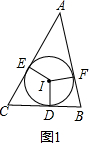
∵⊙I切△ABC于D、E、F,
∴∠CEI=∠CDI=90°,
∵∠C=60°,
∴∠EID=360°-90°-90°-60°=120°,
∵∠EIF=100°,
∴∠FID=360°-120°-100°=140°,
∵⊙I切△ABC于D、E、F,
∴∠IDB=∠IFB=90°,
∴∠B=360°-90°-90°-140°=40°;
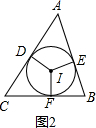 ②当E在AB上,F在BC上,D在AC上时,如图2,
②当E在AB上,F在BC上,D在AC上时,如图2,
∵⊙I切△ABC于D、E、F,
∴∠BEI=∠BFI=90°,
∵∠EIF=100°,
∴∠B=360°-90°-90°-100°=80°;
故答案为:40°或80°.

∵⊙I切△ABC于D、E、F,
∴∠CEI=∠CDI=90°,
∵∠C=60°,
∴∠EID=360°-90°-90°-60°=120°,
∵∠EIF=100°,
∴∠FID=360°-120°-100°=140°,
∵⊙I切△ABC于D、E、F,
∴∠IDB=∠IFB=90°,
∴∠B=360°-90°-90°-140°=40°;
 ②当E在AB上,F在BC上,D在AC上时,如图2,
②当E在AB上,F在BC上,D在AC上时,如图2,∵⊙I切△ABC于D、E、F,
∴∠BEI=∠BFI=90°,
∵∠EIF=100°,
∴∠B=360°-90°-90°-100°=80°;
故答案为:40°或80°.
点评:本题考查了三角形的内切圆和内心,切线的性质的应用,能求出符合条件的所有情况是解此题的关键,用了分类讨论思想,注意:圆的切线垂直于过切点的半径.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
 如图,在等腰Rt△ABC中,∠ACB=90°,点P是△ABC内一点,且CP=1,BP=
如图,在等腰Rt△ABC中,∠ACB=90°,点P是△ABC内一点,且CP=1,BP=| 2 |
| 2 |
| 2 |
| A、①②③ | B、①③④ |
| C、②③④ | D、①②④ |
 如图,边长为a的正三角形的内切圆半径是( )
如图,边长为a的正三角形的内切圆半径是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,⊙O是△ABC的内切圆,D、E、F分别是切点,判定△DEF的形状(按角分类),并说明理由.
如图,⊙O是△ABC的内切圆,D、E、F分别是切点,判定△DEF的形状(按角分类),并说明理由. 如图所示,在Rt△ABC中,∠ACB=90°,AB=BC=2,将Rt△ABC绕A点逆时针旋转45°后得到Rt△ADE,则CD=
如图所示,在Rt△ABC中,∠ACB=90°,AB=BC=2,将Rt△ABC绕A点逆时针旋转45°后得到Rt△ADE,则CD=