题目内容
11．有理数a、b在数轴上的位置如图所示，用不等号填空：
（1）a-b＜0；
（2）a+b＞0；
（3）|a|＜|b|；
（4）$\frac{a}{b}$＞-1．
分析 根据数轴得出a＜0＜b，|a|＜|b|，即可得出答案．
解答 解：数轴得出a＜0＜b，|a|＜|b|，
则（1）a-b＜0；
（2）a+b＞0；
（3）|a|＜|b|；
（4）$\frac{a}{b}$＞-1．
故答案为：（1）＜；（2）＞；（3）＜；（4）＞．
点评 本题考查了数轴，绝对值，相反数，有理数的大小比较的应用，注意：在数轴上表示的数，右边的数总比左边的数大．
练习册系列答案
相关题目
如图，点A、B、C在直线l上，点P在直线l外，PB⊥l于点B，则点P到直线l的距离是线段PB的长度．
2．
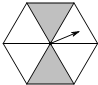如图，一个正六边形转盘被分成6个全等三角形，任意转动这个转盘1次，当转盘停止时，指针指向阴影区域的概率是（ ）
如图，一个正六边形转盘被分成6个全等三角形，任意转动这个转盘1次，当转盘停止时，指针指向阴影区域的概率是（ ）| A． | $\frac{1}{6}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
19．化简$\frac{1+\sqrt{2-\sqrt{2}}+\sqrt{2-\sqrt{3}}}{\sqrt{3}+\sqrt{2+\sqrt{2}}+\sqrt{2+\sqrt{3}}}$，可得（ ）
| A． | $\sqrt{3}$-$\sqrt{2}$ | B． | $\frac{\sqrt{2}+1}{2}$ | C． | 2-$\sqrt{2}$ | D． | $\sqrt{2}$-1 |
如图，8个大小一样的长方形拼成1个大正方形，中间是一个边长为2cm的正方形，同时也可以拼成一个大的长方形，求每个长方形的长和宽．
3．下列各式中，是最简二次根式的是（ ）
| A． | $\sqrt{{a}^{2}+1}$ | B． | $\sqrt{4a}$ | C． | $\sqrt{\frac{1}{5}}$ | D． | $\sqrt{{a}^{4}}$ |
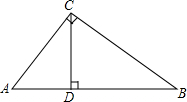如图所示，AC⊥BC，CD⊥AB，AC=5cm，BC=12cm，AB=13cm，则点A到BC的距离是5cm，点C到AB的距离是$\frac{60}{13}$cm．