题目内容
12. 在平面直角坐标系中,若横坐标、纵坐标均为整数点称为格点,若一个多边形的顶点都是格点,则称为格点多边形.记格点多边形的面积为S,其内部的格点数记为n,边界上的格点数记为l,例如图中△ABC是格点三角形,对应的S=1,n=0,l=4.
在平面直角坐标系中,若横坐标、纵坐标均为整数点称为格点,若一个多边形的顶点都是格点,则称为格点多边形.记格点多边形的面积为S,其内部的格点数记为n,边界上的格点数记为l,例如图中△ABC是格点三角形,对应的S=1,n=0,l=4.(1)写出图中格点四边形DEFG对应的S,n,l.
(2)奥地利数学家皮克发现格点多边形的面积可表示为S=n+al+b,其中a,b为常数.
①利用图中条件求a,b的值;
②若某格点多边形对应的n=20,l=15,求S的值;
③在图中画出面积等于5的格点正方形PQRS.
分析 (1)理解题意,观察图形,即可求得结论;
(2)①根据格点三角形ABC及格点四边形DEFG中的S、n、l 的值可得关于a、b的方程组,通过解方程组来求它们的值;
②把相关数值代入①中的关系式进行解答;
③利用①中的函数关系式进行解答.
解答 解:(1)观察图形,可得S=3,n=1,l=6;
(2)①根据格点三角形ABC及格点四边形DEFG中的S、n、l 的值可得$\left\{\begin{array}{l}{4a+b=1}\\{1+6a+b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-1}\end{array}\right.$.
∴S=n+$\frac{1}{2}$l-1;
②将n=20,l=15代入可得S=20+$\frac{1}{2}$×15-1=26.5.
③如图:

点评 此题考查格点图形的面积变化与多边形内部格点数和边界格点数的关系,从简单情况分析,找出规律解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.9的算术平方根是( )
| A. | -3 | B. | 3 | C. | ±3 | D. | 81 |
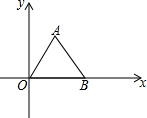 如图,A,B两点的坐标分别是A(1,$\sqrt{3}$),B($\sqrt{5}$,0),则△ABO的面积是$\frac{\sqrt{15}}{2}$.
如图,A,B两点的坐标分别是A(1,$\sqrt{3}$),B($\sqrt{5}$,0),则△ABO的面积是$\frac{\sqrt{15}}{2}$.
 如图,AD是△ABC的高,BE平分∠ABC交AD于E,若∠C=62°,∠BED=66°,求∠BAC的度数.
如图,AD是△ABC的高,BE平分∠ABC交AD于E,若∠C=62°,∠BED=66°,求∠BAC的度数.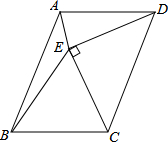 如图,?ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,求∠AEB的度数.
如图,?ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,求∠AEB的度数.