题目内容
13.按一定的规律排列的一列数依次为:$\frac{1}{3}$,$\frac{1}{15}$,$\frac{1}{35}$,$\frac{1}{63}$,…,按此规律排列下去,这列数的第6个数是$\frac{1}{143}$.分析 首先判断出这列数的分子都是1;然后根据3=1×3=(2×1-1)×(2×1+1),15=3×5=(2×2-1)×(2×2+1),35=5×7=(2×3-1)×(2×3+1),63=7×9=(2×4-1)×(2×4+1),…,可得第n个数的分母是(2n-1)(2n+1),所以第n个数是$\frac{1}{(2n-1)(2n+1)}$,据此求出这列数的第6个数是多少即可.
解答 解:因为3=1×3=(2×1-1)×(2×1+1),15=3×5=(2×2-1)×(2×2+1),
35=5×7=(2×3-1)×(2×3+1),63=7×9=(2×4-1)×(2×4+1),…,
所以第n个数的分母是(2n-1)(2n+1),
所以第6个数的分母是:
(2×6-1)×(2×6+1)
=11×13
=143,
所以这列数的第6个数是$\frac{1}{143}$.
故答案为:$\frac{1}{143}$.
点评 此题主要考查了探寻数列规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:第n个数的分母是(2n-1)(2n+1),进而判断出第n个数是$\frac{1}{(2n-1)(2n+1)}$.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
4.9的算术平方根是( )
| A. | -3 | B. | 3 | C. | ±3 | D. | 81 |
18.老王家上个月付话费31元,其月租费为21元,已知市内电话不超过3分钟,每次花费0.18元,如果老王家每次电话不超过3分钟,则老王家至多打电话( )
| A. | 55次 | B. | 56次 | C. | 57次 | D. | 58次 |
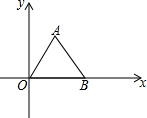 如图,A,B两点的坐标分别是A(1,$\sqrt{3}$),B($\sqrt{5}$,0),则△ABO的面积是$\frac{\sqrt{15}}{2}$.
如图,A,B两点的坐标分别是A(1,$\sqrt{3}$),B($\sqrt{5}$,0),则△ABO的面积是$\frac{\sqrt{15}}{2}$. 如图,AD是△ABC的高,BE平分∠ABC交AD于E,若∠C=62°,∠BED=66°,求∠BAC的度数.
如图,AD是△ABC的高,BE平分∠ABC交AD于E,若∠C=62°,∠BED=66°,求∠BAC的度数.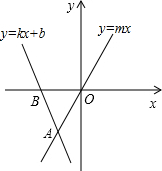 如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为x<-1.
如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为x<-1.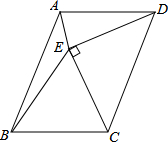 如图,?ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,求∠AEB的度数.
如图,?ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,求∠AEB的度数.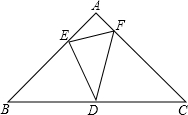 △ABC是等腰直角三角形,∠A=90°,AB=$\sqrt{2}$,点D位于边BC的中点上.点E在AB上,点F在AC上,∠EDF=45°,给出以下结论:
△ABC是等腰直角三角形,∠A=90°,AB=$\sqrt{2}$,点D位于边BC的中点上.点E在AB上,点F在AC上,∠EDF=45°,给出以下结论: