题目内容
11.已知二次函数y=x2+2x+m的图象与x轴有且只有一个公共点,则一元二次不等式x2+2x+m>0的解集为x≠-1.分析 由于二次函数y=x2+2x+m的图象与x轴有且只有一个公共点故△=0,由此得出m的值,进而结合图象得出不等式x2+2x+m>0的解集即可.
解答  解:如图所示:
解:如图所示:
∵二次函数y=x2+2x+m的图象与x轴有且只有一个公共点,
∴△=22-4m=0,
解得:m=1,
故y=x2+2x+1,则图象与x轴交于点(-1,0),
故一元二次不等式x2+2x+m>0的解集为:x≠-1.
故答案为:x≠-1.
点评 本题考查的是抛物线与x轴的交点问题,熟知二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c>0之间的关系是解答此题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
1. 如图,是某校七、八两个年级男生参加课外活动人数扇形,下列说法错误的是( )
如图,是某校七、八两个年级男生参加课外活动人数扇形,下列说法错误的是( )
 如图,是某校七、八两个年级男生参加课外活动人数扇形,下列说法错误的是( )
如图,是某校七、八两个年级男生参加课外活动人数扇形,下列说法错误的是( )| A. | 七年级男生中打篮球活动的人数最多 | |
| B. | 八年级男生中打乒乓球的人数最少 | |
| C. | 七年级男生打乒乓球的人数与八年级男生踢足球的人数一样多 | |
| D. | 两个年级的男生都最喜欢打篮球 |
 如图,过?ABCD对角线AB、BD的交点O作一直线,分别交AB和DC于E、F,交CB和AD的延长线于G、H,求证:DH=BG.
如图,过?ABCD对角线AB、BD的交点O作一直线,分别交AB和DC于E、F,交CB和AD的延长线于G、H,求证:DH=BG.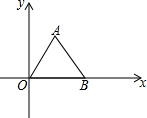 如图,A,B两点的坐标分别是A(1,$\sqrt{3}$),B($\sqrt{5}$,0),则△ABO的面积是$\frac{\sqrt{15}}{2}$.
如图,A,B两点的坐标分别是A(1,$\sqrt{3}$),B($\sqrt{5}$,0),则△ABO的面积是$\frac{\sqrt{15}}{2}$. 如图,AD是△ABC的高,BE平分∠ABC交AD于E,若∠C=62°,∠BED=66°,求∠BAC的度数.
如图,AD是△ABC的高,BE平分∠ABC交AD于E,若∠C=62°,∠BED=66°,求∠BAC的度数.