题目内容
13. 若正三角形的外接圆⊙O的半径为2,求该正三角形的边长.
若正三角形的外接圆⊙O的半径为2,求该正三角形的边长.
分析 连接OB,过O作OD⊥BC于D,求出∠OBD=30°,根据含30度角的直角三角形性质求出OD,根据勾股定理求出BD,根据垂径定理得出BC=2BD,求出即可.
解答 解:如图,连接OB,过O作OD⊥BC于D,
∵⊙O是等边三角形ABC的外接圆,
∴OB平分∠ABC,
∴∠OBD=30°,
∵∠ODB=90°,
∴OD=$\frac{1}{2}$OB=$\frac{1}{2}$×2=1,
在Rt△OBD中,由勾股定理得:BD=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∵OD⊥BC,OD过O,
∴BC=2BD=2DC,
∴BC=2$\sqrt{3}$.
点评 本题考查了等边三角形的性质,勾股定理,含30度角的直角三角形,垂径定理,三角形的外接圆等知识点的综合运用.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
1.用配方法解方程x2-8=2x时,方程可变形为( )
| A. | (x-4)2=9 | B. | (x-1)2=9 | C. | (x+1)2=9 | D. | (x-2)2=9 |
2.用一个平面去截一个正方体,截面的形状不可能是( )
| A. | 梯形 | B. | 长方形 | C. | 六边形 | D. | 七边形 |
 如图,已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AB=FD,证明△ABC≌△FDE.
如图,已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AB=FD,证明△ABC≌△FDE.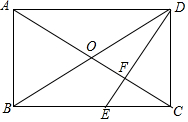 已知:如图,在矩形ABCD中,AB=4cm,BC=8cm,对角线AC与BD交于点O,点E在BC边上,DE与AC交于点F,∠EDC=∠ADB.求:
已知:如图,在矩形ABCD中,AB=4cm,BC=8cm,对角线AC与BD交于点O,点E在BC边上,DE与AC交于点F,∠EDC=∠ADB.求: 如图,△ABC≌△ADE,若∠B=75°,∠C=30°,∠DAC=35°,则∠EAC的度数40°.
如图,△ABC≌△ADE,若∠B=75°,∠C=30°,∠DAC=35°,则∠EAC的度数40°.