题目内容
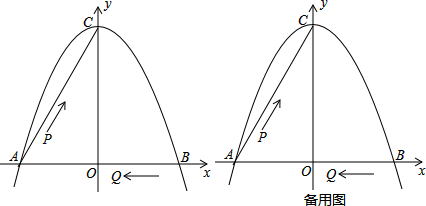
 如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D.
如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D.(1)求证:AE是⊙O的切线;
(2)当BC=4,AB=8时,求劣弧AC的长.
考点:切线的判定,弧长的计算
专题:
分析:(1)连接BC,由AB是⊙O的直径,根据半圆(或直径)所对的圆周角是直角,即可得∠ACB=90°,又由∠EAC=∠D,则可得AE是⊙O的切线;
(2)首先连接OC,易得△OBC是等边三角形,则可得∠AOC=120°,由弧长公式,即可求得劣弧AC的长.
(2)首先连接OC,易得△OBC是等边三角形,则可得∠AOC=120°,由弧长公式,即可求得劣弧AC的长.
解答: 解:(1)连接BC,
解:(1)连接BC,
∵AB是⊙O的直径,
∴∠BAC+∠ABC=90°
又∵∠EAC=∠D,∠B=∠D,
∴∠BAC+∠CAE=90°
即BA⊥AE,
∴AE是⊙O的切线;
 (2)连接CO,
(2)连接CO,
∵△ABC是直角三角形,
∴sin∠BAC=
=
=
,
∴∠BAC=30°,∠ABC=60°,
∴∠AOC=120°,
=
.
 解:(1)连接BC,
解:(1)连接BC,∵AB是⊙O的直径,
∴∠BAC+∠ABC=90°
又∵∠EAC=∠D,∠B=∠D,
∴∠BAC+∠CAE=90°
即BA⊥AE,
∴AE是⊙O的切线;
 (2)连接CO,
(2)连接CO,∵△ABC是直角三角形,
∴sin∠BAC=
| BC |
| AB |
| 4 |
| 8 |
| 1 |
| 2 |
∴∠BAC=30°,∠ABC=60°,
∴∠AOC=120°,
| 120•π×4 |
| 180 |
| 8π |
| 3 |
点评:此题考查了切线的判定、圆周角定理以及弧长公式等知识.此题难度适中,注意数形结合思想的应用,注意辅助线的作法.

练习册系列答案
相关题目
地理老师介绍到:长江比黄河长836千米,黄河长度的6倍比长江长度的5倍多1284千米.小东根据地理教师的介绍,设长江长为x千米,黄河长为y千米,然后通过列、解二元一次方程组,正确地求出了长江和黄河的长度,那么小东列的方程组可能是( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
 若∠1和∠2互余,∠1与∠3互补,∠3=120°,则∠1与∠2的度数分别为( )
若∠1和∠2互余,∠1与∠3互补,∠3=120°,则∠1与∠2的度数分别为( )| A、50°、40° |
| B、60°、30° |
| C、50°、130° |
| D、60°、120° |

 对某市中学生的幸福指数进行调查,从中抽取部分学生的调查表问卷进行统计,并绘制出不完整的统计表和条形统计图.
对某市中学生的幸福指数进行调查,从中抽取部分学生的调查表问卷进行统计,并绘制出不完整的统计表和条形统计图. 如图,直角坐标系中的网格由单位正方形构成,△ABC中,A点坐标为(2,3)
如图,直角坐标系中的网格由单位正方形构成,△ABC中,A点坐标为(2,3)