题目内容
如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A(-1,0),B(3,0),交y轴于C(0,
),连结AC、BC.点P为抛物线上一点,且OP恰好将△ABC的面积二等分.直线OP交边BC于点E,过E点作EN∥AB,交AC于点N.
(1)求二次函数的解析式;
(2)求点P的坐标;
(3)二次函数图象的对称轴上是否存在点F,使得以A,N,F为顶点的三角形与△ABC相似?如果存在,请求出点F的坐标;如果不存在,请说明理由.

| 3 |
(1)求二次函数的解析式;
(2)求点P的坐标;
(3)二次函数图象的对称轴上是否存在点F,使得以A,N,F为顶点的三角形与△ABC相似?如果存在,请求出点F的坐标;如果不存在,请说明理由.

考点:二次函数综合题
专题:
分析:(1)运用待定系数法求解即可.
(2)先求出△ABC的面积,可得出△OBE的面积,运用三角形面积公式求出EH,再运用三角函数求出OH,即可得出点P的坐标;
(3)以A,N,F为顶点的三角形与△ABC相似有三种情况,①若∠AFN=90°②若∠ANF=90°③若∠FAN=90°,针对这种情况进行分析求解得出点F的坐标.
(2)先求出△ABC的面积,可得出△OBE的面积,运用三角形面积公式求出EH,再运用三角函数求出OH,即可得出点P的坐标;
(3)以A,N,F为顶点的三角形与△ABC相似有三种情况,①若∠AFN=90°②若∠ANF=90°③若∠FAN=90°,针对这种情况进行分析求解得出点F的坐标.
解答:解:(1)∵二次函数y=ax2+bx+c(a≠0)的图象交x轴于A(-1,0),B(3,0),交y轴于C(0,
),
∴
,解得
,
∴二次函数的解析式为:y=-
x2+
x+
.
(2)如图1,

∵OA=1,OB=3,OC=
,
∴AC=2,AB=4,BC=2
,
∴△ABC为直角三角形,且∠ACB=90°,∠CAB=60°,∠ABC=30°,
∴S△ABC=
=2
,
∴S△OBE=
,
过E点作EH⊥AC,垂足为H,
∴EH=
=
,
∴BH=EH•tan60°=2,
∴OH=1,
∴E(1,
),
∴直线OE解析式为y=
x,
解
,得
或
,
∴点P的坐标为(
,2)或(-
,-2).
(3)如图2,

由(1)(2)知二次函数y=-
x2+
x+
的对称轴为x=1,且∠ACB=90°.
∵EH=
,OC=
,AC=2,且EN∥AB,
∴
=
即
=
∴AN=
,
①若∠AFN=90°,
∵AN的中点到对称轴的距离大于1,而
AN=
<1,
∴以AN为直径的圆不与对称轴相交,
∴∠AFN≠90°,即此时不存在符合条件的F点.
②若∠ANF=90°,当∠NAF=60°,则F,H重合,此时∠ANF≠90°,
当∠NAF=30°,则F,E重合,
此时∠ANF≠90°,即此时不存在符合条件的F点,
③若∠FAN=90°,作AF⊥AN交对称轴于点F,此时,∠HAF=30°,AH=2,HF=
,
AF=
,而AN=
,
∴∠AFN=30°,
∴△ANF∽△ABC,
∴F(1,-
).
| 3 |
∴
|
|
∴二次函数的解析式为:y=-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
(2)如图1,

∵OA=1,OB=3,OC=
| 3 |
∴AC=2,AB=4,BC=2
| 3 |
∴△ABC为直角三角形,且∠ACB=90°,∠CAB=60°,∠ABC=30°,
∴S△ABC=
4×
| ||
| 2 |
| 3 |
∴S△OBE=
| 3 |
过E点作EH⊥AC,垂足为H,
∴EH=
| 2S△OBE |
| OB |
2
| ||
| 3 |
∴BH=EH•tan60°=2,
∴OH=1,
∴E(1,
2
| ||
| 3 |
∴直线OE解析式为y=
2
| ||
| 3 |
解
|
|
|
∴点P的坐标为(
| 3 |
| 3 |
(3)如图2,

由(1)(2)知二次函数y=-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
∵EH=
2
| ||
| 3 |
| 3 |
∴
| AC |
| AN |
| CO |
| EH |
| 2 |
| AN |
| ||||
|
∴AN=
| 4 |
| 3 |
①若∠AFN=90°,
∵AN的中点到对称轴的距离大于1,而
| 1 |
| 2 |
| 2 |
| 3 |
∴以AN为直径的圆不与对称轴相交,
∴∠AFN≠90°,即此时不存在符合条件的F点.
②若∠ANF=90°,当∠NAF=60°,则F,H重合,此时∠ANF≠90°,
当∠NAF=30°,则F,E重合,
此时∠ANF≠90°,即此时不存在符合条件的F点,
③若∠FAN=90°,作AF⊥AN交对称轴于点F,此时,∠HAF=30°,AH=2,HF=
2
| ||
| 3 |
AF=
4
| ||
| 3 |
| 4 |
| 3 |
∴∠AFN=30°,
∴△ANF∽△ABC,
∴F(1,-
2
| ||
| 3 |
点评:本题主要考查了二次函数与方程、几何知识的综合应用,解题的关键是善于将函数问题利用几何图形的有关性质、定理和二次函数的知识求解,特别第3小题必须分三种情况讨论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列各条件不能判断四边形ABCD是矩形的是( )
| A、∠A=∠B=∠C=90° |
| B、AC=BD且AC与BD互相平分 |
| C、AB∥CD,AC=BD |
| D、AB∥CD,AB=CD,AB⊥BC |
 如图,直线AB和CD相交于点O,∠AOD和∠BOC的和为202°,那么∠AOC的度数为( )
如图,直线AB和CD相交于点O,∠AOD和∠BOC的和为202°,那么∠AOC的度数为( )| A、89° | B、101° |
| C、79° | D、110° |
如果把
的x与y值都扩大10倍,那么这个分式的值( )
| 5x |
| x+y |
| A、缩小10倍 | B、扩大50倍 |
| C、扩大10倍 | D、不变 |




 在平面直角坐标系中,描出下列各点,并将各点用线段依次连接起来:(2,1)(6,1)(6,3)(7,3)(4,6)(1,3)(2,3)观察得到的图形,你觉得它像什么?
在平面直角坐标系中,描出下列各点,并将各点用线段依次连接起来:(2,1)(6,1)(6,3)(7,3)(4,6)(1,3)(2,3)观察得到的图形,你觉得它像什么? 如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D.
如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D.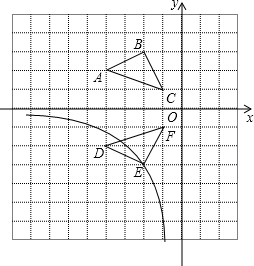 如图,在边为的1正方形组成的网格中,建立平面直角坐标系,若A(-4,2)、B(-2,3)、C(-1,1),将△ABC沿着x轴翻折后,得到△DEF,点B的对称点是点E,求过点E的反比例函数解析式,并写出第三象限内该反比例函数图象所经过的所有格点的坐标.
如图,在边为的1正方形组成的网格中,建立平面直角坐标系,若A(-4,2)、B(-2,3)、C(-1,1),将△ABC沿着x轴翻折后,得到△DEF,点B的对称点是点E,求过点E的反比例函数解析式,并写出第三象限内该反比例函数图象所经过的所有格点的坐标.