题目内容
11.如果关于x的分式方程$\frac{a}{x-1}$-5=$\frac{x-3}{1-x}$有正数解,且关于x的不等式组$\left\{\begin{array}{l}{a-2x≤1-x}\\{\frac{4x+1}{2}>x+3}\end{array}\right.$的解集为x>$\frac{5}{2}$,那么符合条件的所有整数a的和为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 先将分式方程和不等式分别解出,然后求出a的范围即可求出所有整数a的和.
解答 解:∵$\frac{a}{x-1}$-5=$\frac{x-3}{1-x}$,
∴a-5(x-1)=-(x-3)
∴x=$\frac{a+2}{4}$
将x=$\frac{a+2}{4}$代入x-1≠0,
∴$\left\{\begin{array}{l}{\frac{a+2}{4}>0}\\{\frac{a+2}{4}-1≠0}\end{array}\right.$
解得:a>-2且a≠2
∵$\left\{\begin{array}{l}{a-2x≤1-x}\\{\frac{4x+1}{2}>x+3}\end{array}\right.$
∴解得:x>a-1且x>$\frac{5}{2}$
∵该不等式组的解集为x>$\frac{5}{2}$,
∴a-1≤$\frac{5}{2}$,
∴a≤$\frac{7}{2}$,
∴a的范围是:-2<a≤$\frac{7}{2}$且a≠2,
∵a是整数,
∴a=-1,0,1,3
∴符合条件的所有整数a的和为:3
故选(B)
点评 本题考查分式方程以及不等式组的解法,解题的关键是熟练运用分式方程以及不等式组的解法,本题属于中等题型.

练习册系列答案
相关题目
1.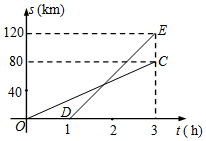 已知A,B两地相距80km,甲,乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲,乙离开A地的路程s(km)与时间t(h)的函数关系,根据图象得出的下列信息错误的是( )
已知A,B两地相距80km,甲,乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲,乙离开A地的路程s(km)与时间t(h)的函数关系,根据图象得出的下列信息错误的是( )
 已知A,B两地相距80km,甲,乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲,乙离开A地的路程s(km)与时间t(h)的函数关系,根据图象得出的下列信息错误的是( )
已知A,B两地相距80km,甲,乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲,乙离开A地的路程s(km)与时间t(h)的函数关系,根据图象得出的下列信息错误的是( )| A. | 乙到达B地时甲距A地120km | B. | 乙出发1.8小时被甲追上 | ||
| C. | 甲,乙相距20km时,t为2.4h | D. | 甲的速度是乙的速度的$\frac{9}{4}$倍 |
2.假设有足够多的黑白围棋子,摆成一个“中”字,下列图形中,第①个图形中有4 枚黑子和4枚白子,第②个图形中有6枚黑子和11枚白子,第③个图形中有8枚黑子和18枚白子,…,按此规律排列,则第⑧个图形中黑子和白子的枚数分别为( )


| A. | 14和48 | B. | 16和48 | C. | 18和53 | D. | 18和67 |
19. 如图,AO⊥BO,CO⊥DO,∠AOC:∠BOC=1:4,则∠BOD=( )
如图,AO⊥BO,CO⊥DO,∠AOC:∠BOC=1:4,则∠BOD=( )
 如图,AO⊥BO,CO⊥DO,∠AOC:∠BOC=1:4,则∠BOD=( )
如图,AO⊥BO,CO⊥DO,∠AOC:∠BOC=1:4,则∠BOD=( )| A. | 105° | B. | 120° | C. | 135° | D. | 150° |
6.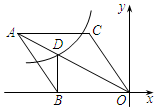 如图,在平面直角坐标系xOy中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-3,4),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
如图,在平面直角坐标系xOy中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-3,4),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
 如图,在平面直角坐标系xOy中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-3,4),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
如图,在平面直角坐标系xOy中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-3,4),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )| A. | $-\frac{50}{3}$ | B. | $-\frac{25}{2}$ | C. | -12 | D. | $-\frac{25}{4}$ |
16.下列计算正确的是( )
| A. | 2a+3b=5ab | B. | $\sqrt{12}$-$\sqrt{3}$=$\sqrt{3}$ | C. | (a+b)2=a2+b2 | D. | a6÷a3=a2 |
20.下列四个数中,无理数是( )
| A. | $\frac{1}{3}$ | B. | $\sqrt{2}$ | C. | 0 | D. | |-5| |