题目内容
19.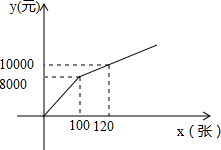 为丰富群众的业余生活,我市准备组织篮球比赛,市体育局策划本次活动,在与单位协商团购票时推出两种方案.设购买门票数为x(张),总费用为y(元).方案一:若单位赞助广告费8000元,则该单位所购门票的价格为每张50元;(总费用=广告赞助费+门票费)
为丰富群众的业余生活,我市准备组织篮球比赛,市体育局策划本次活动,在与单位协商团购票时推出两种方案.设购买门票数为x(张),总费用为y(元).方案一:若单位赞助广告费8000元,则该单位所购门票的价格为每张50元;(总费用=广告赞助费+门票费)方案二:直接购买门票方式如图所示.解答下列问题:
(1)方案一中,y与x的函数关系式为y=8000+50x;
方案二中,当0≤x≤100时,y与x的函数关系式为y=80x,
当x>100时,y与x的函数关系式为y=100x-2000;
(2)如果购买本场篮球赛门票超过100张,你将选择哪一种方案,使总费用最省?请说明理由.
分析 (1)方案一中,总费用=广告赞助费8000+门票单价50×票的张数;
方案二中,当0≤x≤100时,应先算出门票的单价,进而乘以张数即可;
当x>100时,设出一次函数解析式,把其中两点的坐标代入即可求得相应的函数解析式;
(2)让方案一的函数解析式和方案二中第2个解析式的函数值相等,可得两个方案的费用相同的自变量的值,进而可得总费用最省的方案.
解答 解:(1)方案一:赞助费为8000,每张门票费用为50,
∴y=8000+50x;
方案二:当0≤x≤100时,门票单价为8000÷100=80元,
∴y=80x;
当x>100时,
设解析式为y=kx+b,
$\left\{\begin{array}{l}{100k+b=8000}\\{120k+b=10000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=100}\\{b=-2000}\end{array}\right.$.
∴y=100x-2000.
故答案为y=8000+50x;y=80x;y=100x-2000.
(2)由题意得:8000+50x=100x-2000
解得x=200,
8000+50x>100x-2000
解得x<200,
8000+50x<100x-2000
解得x>200
答:当100<x<200时,选择方案二总费用最省;
当x=200时,方案一、二均可;
当x>200时,选择方案一,总费用最省.
点评 考查一次函数的应用;根据自变量不同的取值,对总门票费分情况进行探讨是解决本题的易错点.

练习册系列答案
相关题目
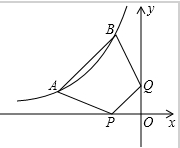 如图,A(a,1),B(-1,b)都在双曲线y=-$\frac{3}{x}$(x>0)点P,Q分别是x轴,y轴上的动点,当四边形PABQ的周长最小值时,PQ所在直线的解析式是y=x+2.
如图,A(a,1),B(-1,b)都在双曲线y=-$\frac{3}{x}$(x>0)点P,Q分别是x轴,y轴上的动点,当四边形PABQ的周长最小值时,PQ所在直线的解析式是y=x+2.
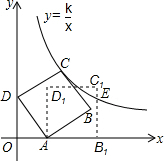 如图,在平面直角坐标系中,边长为5的正方形ABCD斜靠在y轴上,顶点A(3,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,得正方形AB1C1D1,且B1恰好落在x轴的正半轴上,此时边B1C1交反比例图象于点E,则点E的纵坐标是( )
如图,在平面直角坐标系中,边长为5的正方形ABCD斜靠在y轴上,顶点A(3,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,得正方形AB1C1D1,且B1恰好落在x轴的正半轴上,此时边B1C1交反比例图象于点E,则点E的纵坐标是( )